Intensity at centre in YDSE is l0 if one slit is covered. Then intensity at centre will be
2I
5I
(5+2√2)I
(5+4√2)I
The correct Answer is:A
Location of the point y=ω4=λD4d
⇒Δx=ydD=λ4
⇒ϕ=2πλ.Δx=π2
∵IR=I1+I2+2√I1I2cosϕ
∴4I=2I+I2+0
⇒I2=2I
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion reason8videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - match column4videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Check point65videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER22videos
SOLVED PAPERS 2018
Similar Questions
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The Intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be
View SolutionIn a Young's double-slit expriment using identical slits, the intensity at a bright fringe is I_(0). If one of the slits is now covered, the intensity at any point on the screen will be
View SolutionIn a YDSE with identical slits, the intensity of the central bright fringe is I0. If one of the slits is covered, the intensity at the same point is
View SolutionIn Young's double slit experiment with light of wavelength λ=600nm, intensity of central fringe is I0. Now one of the slit is covered by glass plate of refractive index 1.4 and thickness t=5μm. The new intensity at the same point on screen will be :
View SolutionIntensity at centre in YDSE is l0 if one slit is covered. Then intensity at centre will be
View SolutionIn YDSE, both slits produce equal intensities on the screen. A 100% transparent thin film is placed in front of one of the slits. Now, the intensity on the centre becomes 75% of the previous intensity. The wavelength of light is 6000Å and refractive index of glass is 1.5. Thus, minimum thickness of the glass slab is
View SolutionIn a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionIn a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionIn a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
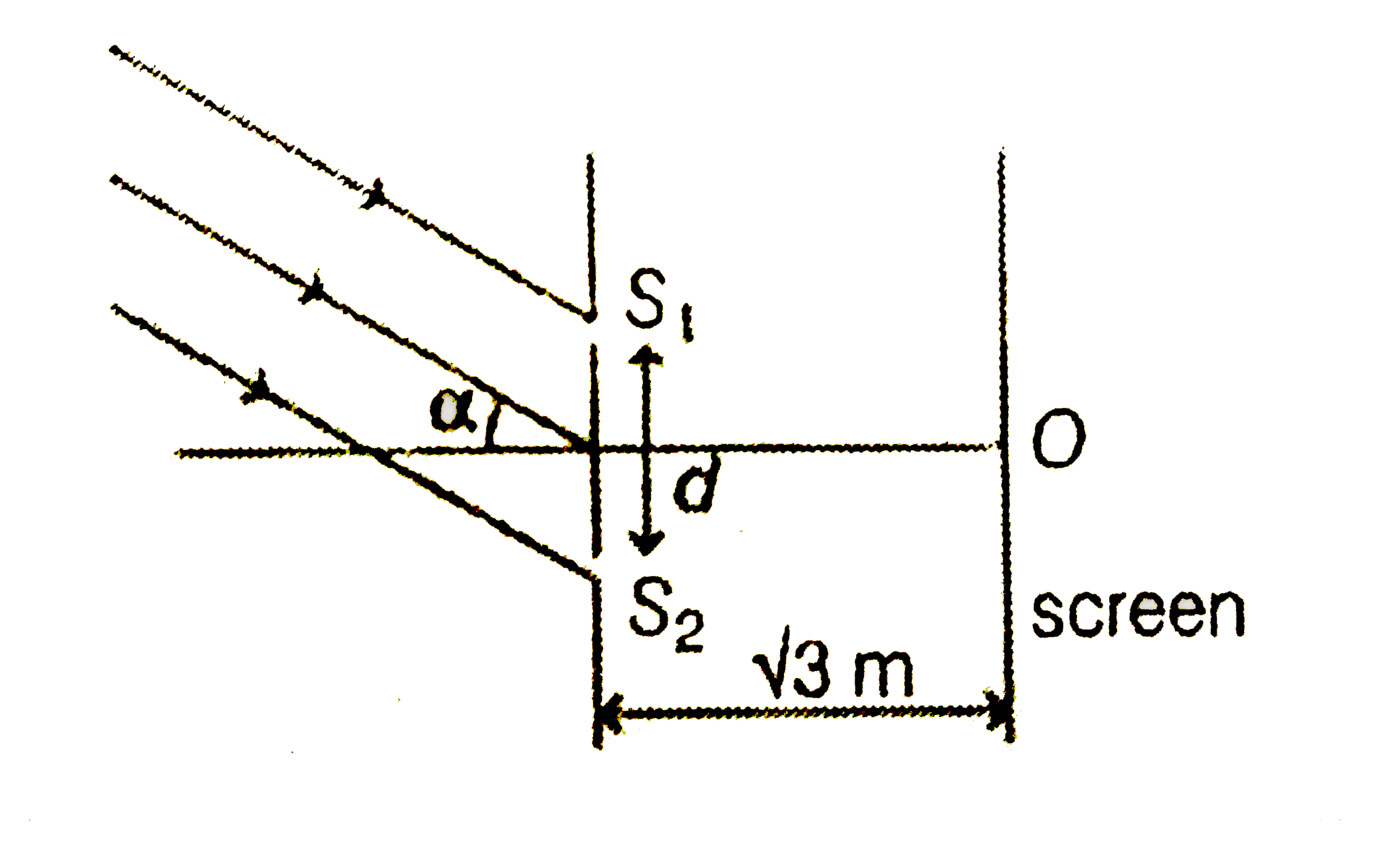
View SolutionA parrallel beam of light (λ=5000Å) is incident at an angle α=30∘ as shown in YDSE experiment. Intensity due to each slit at any point on screen in I0. The distance between slits is 1mm. The intensity at central point O on the screen is KI0. Find the value of K.
 View Solution
View Solution

