The magnetic potential energy stored in a certain inductor is 25mJ, when the current in the inductor is 60mA. This inductor is of inductance
1.389 H
138.88 H
0.138 H
13.89 H
The correct Answer is:D
To find the inductance of the inductor given the magnetic potential energy and the current, we can follow these steps:
Step 1: Write down the given values
- Magnetic potential energy (U) = 25 mJ = 25×10−3 J
- Current (I) = 60 mA = 60×10−3 A
Step 2: Use the formula for magnetic potential energy
The formula for magnetic potential energy stored in an inductor is given by:
U=12LI2
where:
- U is the magnetic potential energy,
- L is the inductance,
- I is the current.
Step 3: Rearrange the formula to solve for inductance (L)
We can rearrange the formula to solve for L:
L=2UI2
Step 4: Substitute the known values into the formula
Now we substitute the values of U and I into the equation:
L=2×(25×10−3)(60×10−3)2
Step 5: Calculate I2
First, calculate I2:
I2=(60×10−3)2=3600×10−6=3.6×10−3
Step 6: Substitute I2 back into the equation for L
Now, substitute I2 back into the equation for L:
L=2×(25×10−3)3.6×10−3
Step 7: Calculate L
Now, perform the calculation:
L=50×10−33.6×10−3=503.6≈13.89H
Step 8: Final answer
Thus, the inductance L is approximately 13.89H.
- Magnetic potential energy (U) = 25 mJ = 25×10−3 J
- Current (I) = 60 mA = 60×10−3 A
The formula for magnetic potential energy stored in an inductor is given by:
U=12LI2
where:
- U is the magnetic potential energy,
- L is the inductance,
- I is the current.
We can rearrange the formula to solve for L:
L=2UI2
Now we substitute the values of U and I into the equation:
L=2×(25×10−3)(60×10−3)2
First, calculate I2:
I2=(60×10−3)2=3600×10−6=3.6×10−3
Now, substitute I2 back into the equation for L:
L=2×(25×10−3)3.6×10−3
Now, perform the calculation:
L=50×10−33.6×10−3=503.6≈13.89H
Thus, the inductance L is approximately 13.89H.
Topper's Solved these Questions
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - AIIMS
22 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - Assertion and Reasons
10 Videos
- SOLVED PAPER 2017BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)
32 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions
13 Videos
Similar Questions
A capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionAn L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4x10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View Solution
Knowledge Check
The energy stored in an inductor of self-inductance L henry carrying a current of I ampere is
A12L2IB12LI2CLI2DL2I
The frequency of oscillation of current in the inductor is -
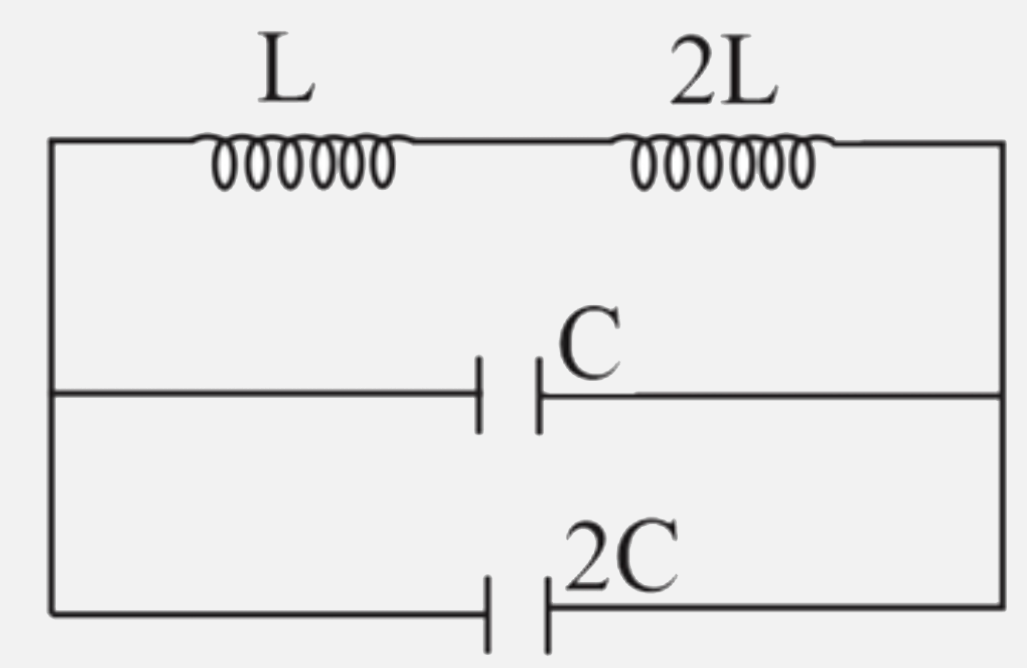
View SolutionThe frequency of oscillation of current in the inductor is:
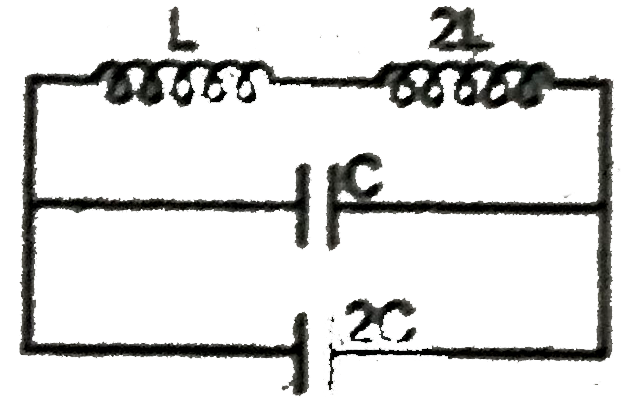
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
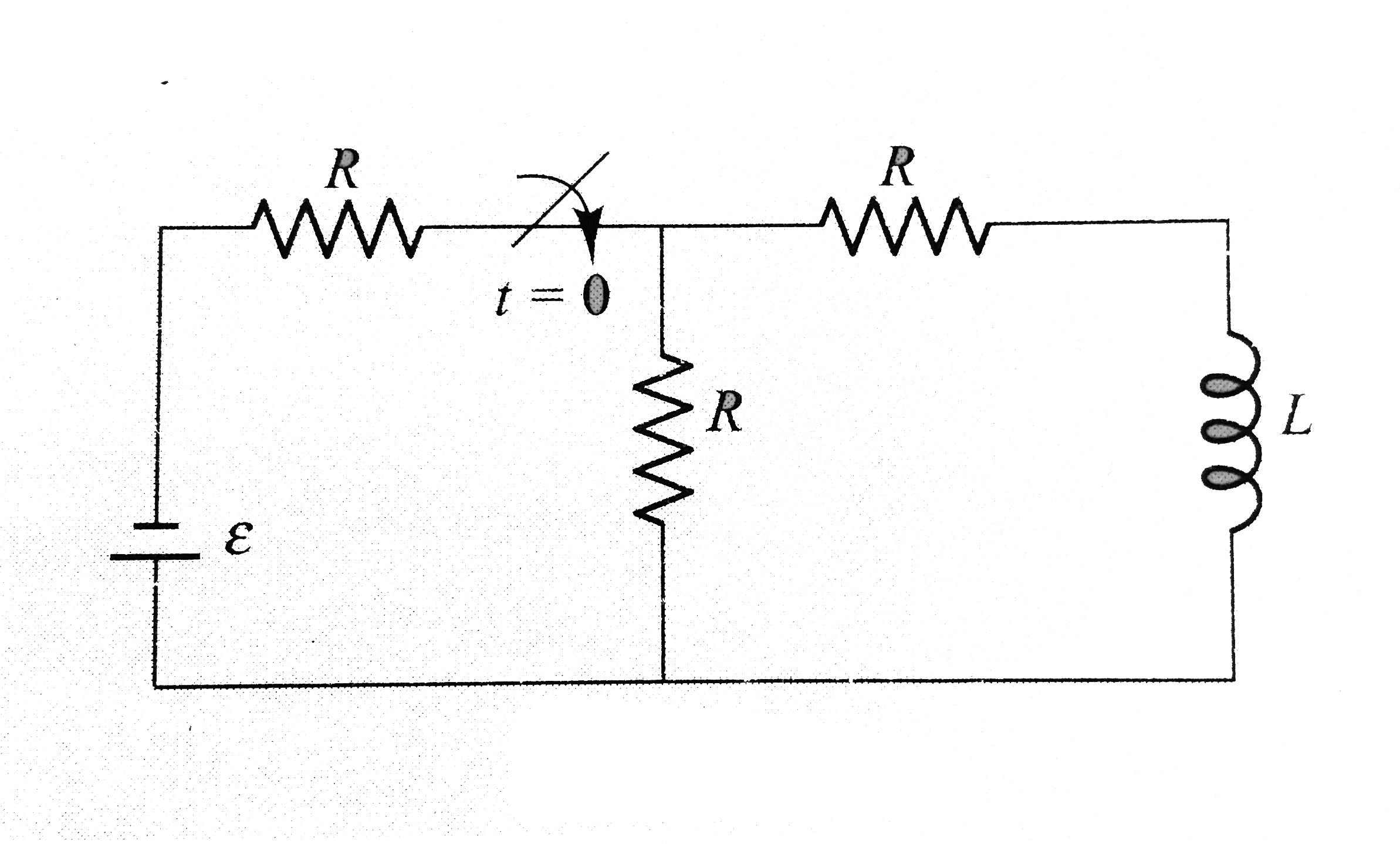
View SolutionThe energy stored in an inductor of self inductance L carrying current l, is given by
View SolutionCalculate the energy stored in an inductor of inductance 50 mH when a current of 2.0 A is passed through it.
View SolutionObtain the expression for the magnetic energy stored in an ideal inductor of self inductance L when a current I passes through it.
Hence obtain the expression for the energy density of magentic field produced in the inductor.
View SolutionThe energy stored in an inductor of self-inductance L henry carrying a current of I ampere is
View Solution
