A capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
2π√LC
12π√LC
π√LC2
12π√LC
The correct Answer is:C
To solve the problem, we need to find the time t at which the energy stored in the capacitor is equal to the energy stored in the inductor. Let's break down the solution step by step.
Step 1: Understanding the initial conditions
At time t=0, the charge on the capacitor is given as:
q(0)=1√2qmax
where qmax is the maximum charge on the capacitor.
Step 2: Relating charge to time
The charge q(t) on the capacitor at any time t in an LC circuit is given by:
q(t)=qmaxsin(ωt+ϕ)
where ω=1√LC and ϕ is the phase constant.
Step 3: Finding the phase constant ϕ
At t=0:
q(0)=qmaxsin(ϕ)=1√2qmax
This implies:
sin(ϕ)=1√2⟹ϕ=π4
Step 4: Current in the circuit
The current I(t) in the circuit can be found by differentiating q(t):
I(t)=dqdt=ωqmaxcos(ωt+ϕ)
Substituting ϕ=π4:
I(t)=ωqmaxcos(ωt+π4)
Step 5: Energy stored in the capacitor and inductor
The energy stored in the capacitor UC is given by:
UC=12q2C
The energy stored in the inductor UL is given by:
UL=12LI2
Step 6: Setting the energies equal
We need to find t such that:
UC=UL
Substituting the expressions for UC and UL:
12q2C=12LI2
Substituting I(t):
q2C=L(ωqmaxcos(ωt+π4))2
Step 7: Substituting q(t)
Substituting q(t)=qmaxsin(ωt+π4):
(qmaxsin(ωt+π4))2C=L(ωqmaxcos(ωt+π4))2
Step 8: Simplifying the equation
Cancelling q2max from both sides:
sin2(ωt+π4)C=Lω2cos2(ωt+π4)
Substituting ω2=1LC:
sin2(ωt+π4)C=LLCcos2(ωt+π4)
This simplifies to:
sin2(ωt+π4)=cos2(ωt+π4)
Step 9: Using trigonometric identities
This implies:
tan2(ωt+π4)=1⟹tan(ωt+π4)=1
Thus:
ωt+π4=π4+nπ(n∈Z)
Taking n=1:
ωt+π4=5π4⟹ωt=π⟹t=πω
Step 10: Final expression for time
Substituting ω=1√LC:
t=π1√LC=π√LC
Final Answer
Thus, the time t at which the energy stored in the capacitor is equal to the energy stored in the inductor is:
t=π2√LC
At time t=0, the charge on the capacitor is given as:
q(0)=1√2qmax
where qmax is the maximum charge on the capacitor.
The charge q(t) on the capacitor at any time t in an LC circuit is given by:
q(t)=qmaxsin(ωt+ϕ)
where ω=1√LC and ϕ is the phase constant.
At t=0:
q(0)=qmaxsin(ϕ)=1√2qmax
This implies:
sin(ϕ)=1√2⟹ϕ=π4
The current I(t) in the circuit can be found by differentiating q(t):
I(t)=dqdt=ωqmaxcos(ωt+ϕ)
Substituting ϕ=π4:
I(t)=ωqmaxcos(ωt+π4)
The energy stored in the capacitor UC is given by:
UC=12q2C
The energy stored in the inductor UL is given by:
UL=12LI2
We need to find t such that:
UC=UL
Substituting the expressions for UC and UL:
12q2C=12LI2
Substituting I(t):
q2C=L(ωqmaxcos(ωt+π4))2
Substituting q(t)=qmaxsin(ωt+π4):
(qmaxsin(ωt+π4))2C=L(ωqmaxcos(ωt+π4))2
Cancelling q2max from both sides:
sin2(ωt+π4)C=Lω2cos2(ωt+π4)
Substituting ω2=1LC:
sin2(ωt+π4)C=LLCcos2(ωt+π4)
This simplifies to:
sin2(ωt+π4)=cos2(ωt+π4)
This implies:
tan2(ωt+π4)=1⟹tan(ωt+π4)=1
Thus:
ωt+π4=π4+nπ(n∈Z)
Taking n=1:
ωt+π4=5π4⟹ωt=π⟹t=πω
Substituting ω=1√LC:
t=π1√LC=π√LC
Thus, the time t at which the energy stored in the capacitor is equal to the energy stored in the inductor is:
t=π2√LC
Similar Questions
Find the charge stored in the capacitor.
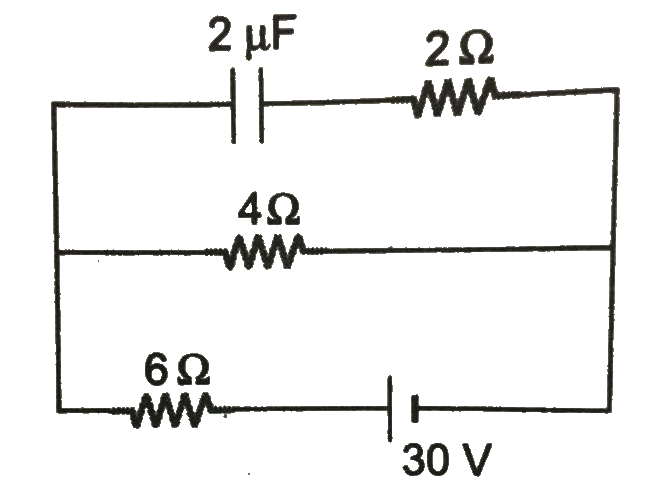
View SolutionIn the steady state of the circuit shown in the figure the ratio of energy stored in the inductor to th energy stored in the capacitor is 1000000.

View SolutionIn oscillating Lc circuit, the total stored energy is U and maximum charge upon capacitor is Q2, the energy stored in the inductor is
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionThe current in 1Ω resistance and charge stored in the capacitor are
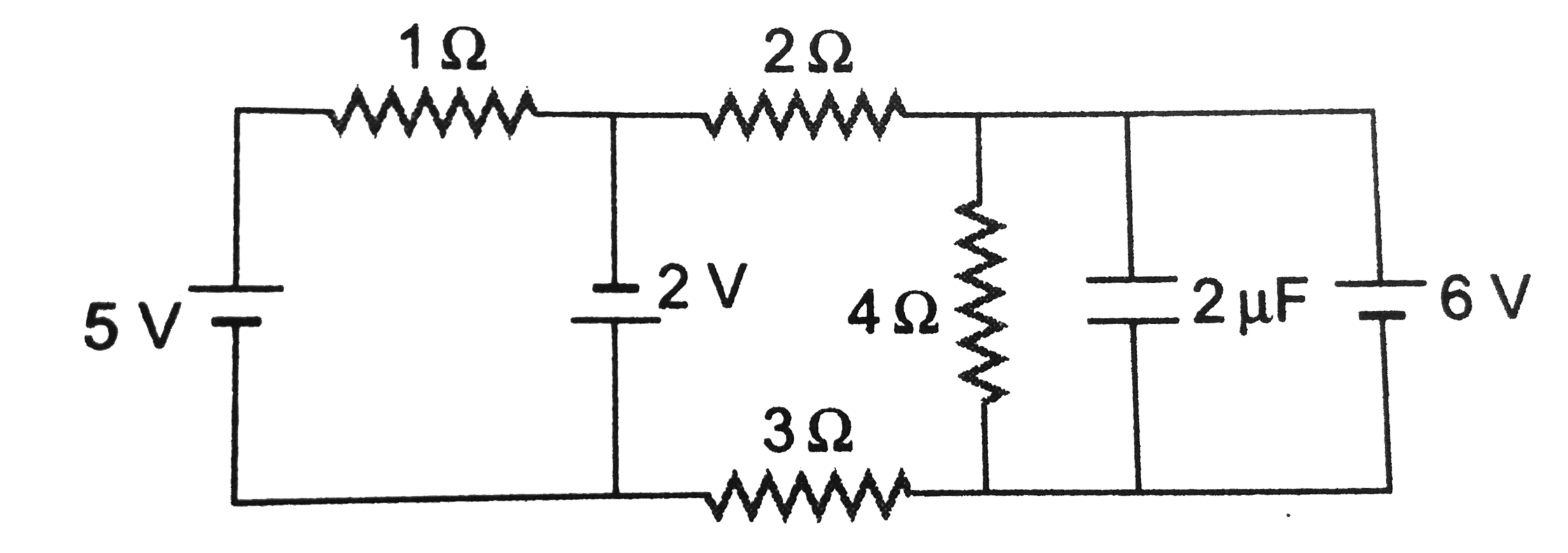
View SolutionThe capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of charge on the capacitor?
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
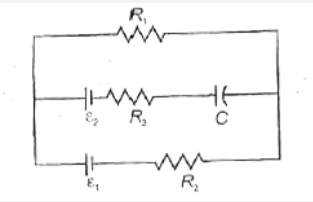
View Solution
