A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If λ=648nm, obtain the least value of t(in10−8m) which the rays interface constructively.
To solve the problem, we will follow these steps:
Step 1: Understand the conditions for constructive interference
For constructive interference to occur, the path difference between the two reflected rays must be an integral multiple of the wavelength. Additionally, we need to account for the phase change that occurs when light reflects off a medium with a higher refractive index.
Step 2: Calculate the path difference
When light reflects off the upper surface of the thin layer (refractive index 1.8), there is a phase change of λ/2 (half a wavelength). The path difference between the two rays (one reflecting off the upper surface and one reflecting off the lower surface) is given by:
Path difference=2μt
where μ is the refractive index of the thin layer, and t is the thickness of the layer.
Step 3: Set up the equation for constructive interference
For constructive interference, the total path difference must satisfy:
2μt+λ2=nλ
where n is an integer (1, 2, 3,...).
Step 4: Rearrange the equation
Rearranging the equation gives:
2μt=nλ−λ2
2μt=(n−12)λ
Step 5: Solve for t
Now, we can solve for t:
t=(n−12)λ2μ
Step 6: Substitute values
Given:
- λ=648nm=648×10−9m
- μ=1.8
For the least value of t, we take n=1:
t=(1−12)⋅648×10−92⋅1.8
t=0.5⋅648×10−93.6
t=324×10−93.6
t=90×10−9m
Step 7: Convert to the required format
To express t in 10−8m:
t=90×10−9m=9×10−8m
Final Answer
The least value of t in 10−8m is:
9
For constructive interference to occur, the path difference between the two reflected rays must be an integral multiple of the wavelength. Additionally, we need to account for the phase change that occurs when light reflects off a medium with a higher refractive index.
When light reflects off the upper surface of the thin layer (refractive index 1.8), there is a phase change of λ/2 (half a wavelength). The path difference between the two rays (one reflecting off the upper surface and one reflecting off the lower surface) is given by:
Path difference=2μt
where μ is the refractive index of the thin layer, and t is the thickness of the layer.
For constructive interference, the total path difference must satisfy:
2μt+λ2=nλ
where n is an integer (1, 2, 3,...).
Rearranging the equation gives:
2μt=nλ−λ2
2μt=(n−12)λ
Now, we can solve for t:
t=(n−12)λ2μ
Given:
- λ=648nm=648×10−9m
- μ=1.8
t=(1−12)⋅648×10−92⋅1.8
t=0.5⋅648×10−93.6
t=324×10−93.6
t=90×10−9m
To express t in 10−8m:
t=90×10−9m=9×10−8m
The least value of t in 10−8m is:
9
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
The outer surface of a transparent glass slab of refractive index μS=1.5 is coated by a thin layer of transparent medium of refractive index μC=1.6. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of the coat interfere destructively. If thickness of the coat is 5K×10−8m, calculate the minimum value of K.
View SolutionA glass prism of refractive index 1.5 is immersed in water of refractive index 4/3. A light ray incident normally on face AB is totally reflected at face AC if

View SolutionWhite light is incident normally on a glass plate (in air) of thickness 500nm and refractive index of 1.5. The wavelength (in nm) in the visible region (400nm−700nm) that is strongly reflected by the plate is:
View SolutionA ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is
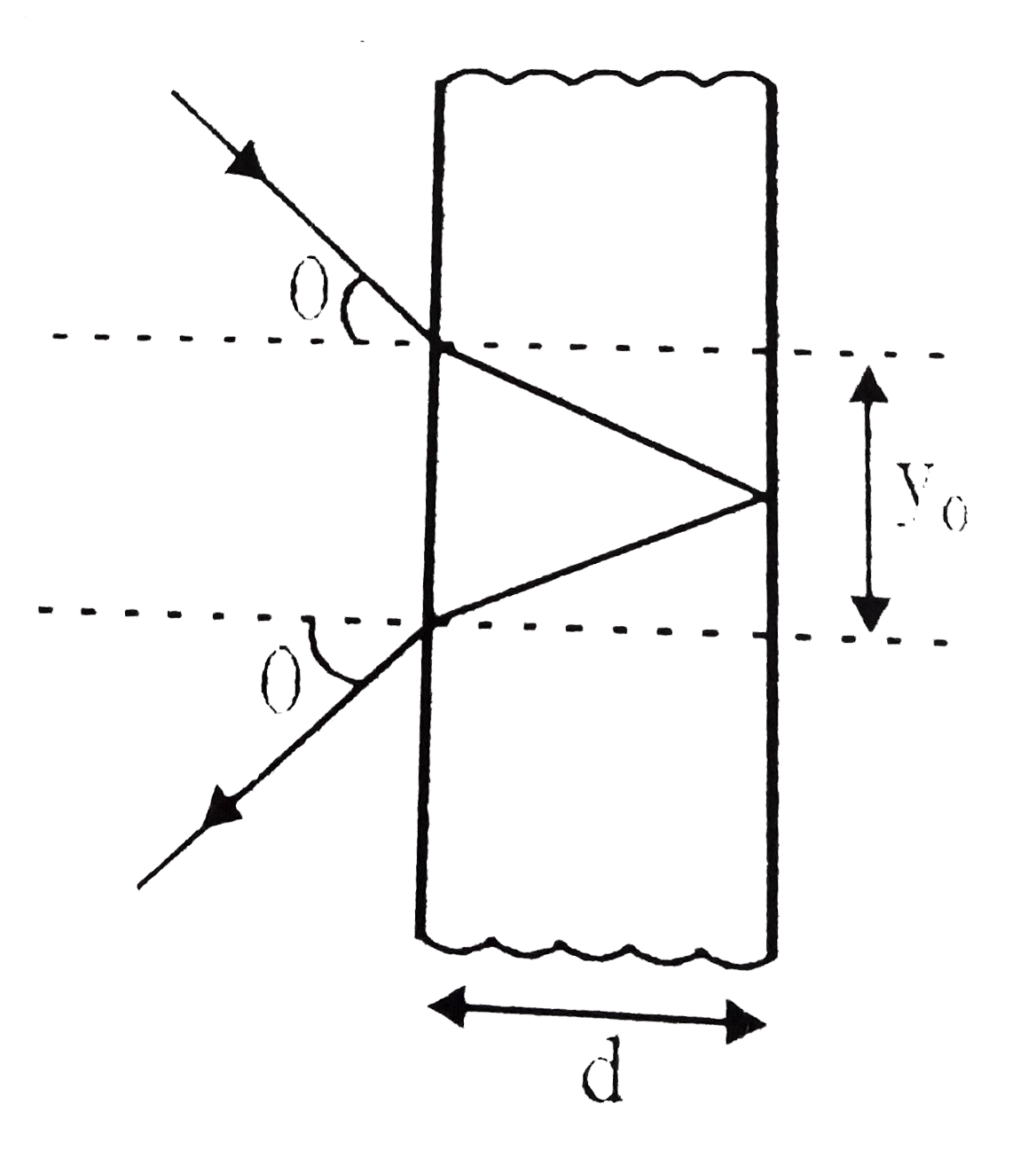
View SolutionOrdinary (i.e., unpolarised) lights is incident on the surface of a transparent material at the polarising angle. If it is partly reflected and partly refracted, what is the angle between the reflected and the refracted rays?
View SolutionA cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by

View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3) . A light beam normally on the face AB is totally reflected to reach on the face BC if

View SolutionWhen white light is incident normally an oil film of thickness 10−4cm and refractive index. 1.4 then the wavelength which will not be seen in the reflected system of light is
View SolutionConsider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
View SolutionConsider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
View Solution
