Explain close packing in two dimensions.
The close packing in two dimensions can be done in two ways by stacking the rows of closed packed spheres : (i) Square Close Packing (ii) Hexagonal Close Packing (HCP)
(i) Square Close Packing : In square close packing, the spheres of second row are placed exactly above the spheres of first row such that spheres of these two rows are aligned horizontally as well as vertically.
If the first row of spheres is called "A" type row, the second row being exactly the same as the first one is also of ..A.. type and hence by placing more rows, AAAA..... type of arrangement is obtained.
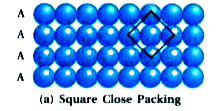
In this arrangement, each sphere is in contact with four of its neighbours and hence the coordination number of a sphere is four.
If the centres of the four immediate neighbours are joined a square is formed and hence it is named Square Closed Packing.
(ii) Hexagonal Closed Packing (HCP) :

In hexagonal close packing, the spheres of second row are fit in the depressions of the spheres of first row.
If the spheres of first row is called ..A.. type, the one in second row may be called ..B.. type.
The spheres of third row are placed in depressions of the spheres of second row such that spheres of first row and third row are in same alignment horizontally and vertically.
As the third row is exactly same as that of first row it is called ..A.. type. Hence, we get ABABAB .... type of arrangement.
In this arrangement each sphere is in contact with six of its neighbour and thus in two dimensional the co-ordination number is six. The centres of these six spheres are at the corners of regular hexagon hence this packing is called two dimensional hexagonal close packing.
In this arrangement, there is less free space and so this packing is more efficient than square close packing.
The empty spaces called voids are surrounded by three spheres in this arrangement. The centres of these three touching spheres form a triangle and hence it is called Triangular Voids. In one row, the apex of the triangles are pointed upwards and in the next layer dowards. Hence, we get two types of triangular voids.
Topper's Solved these Questions
- THE SOLID STATEBOOK - KUMAR PRAKASHANCHAPTER - THE SOLID STATEEXERCISE - SECTION - A (EXAMPLES)
5 Videos
- THE SOLID STATEBOOK - KUMAR PRAKASHANCHAPTER - THE SOLID STATEEXERCISE - SECTION - B (INTEXT QUESTIONS AND ANSWERS)
23 Videos
- THE SOLID STATEBOOK - KUMAR PRAKASHANCHAPTER - THE SOLID STATEEXERCISE - SECTION - E (MULTIPLE CHOICE QUESTIONS)(MCQs ASKED IN BOARD EXAMS)
35 Videos
- THE P-BLOCK ELEMENTS BOOK - KUMAR PRAKASHANCHAPTER - THE P-BLOCK ELEMENTS EXERCISE - SECTION-E (MULTIPLE CHOICE QUESTIONS (MCQS)) (MCQS ASKED IN BOARD EXAM)
77 Videos
Similar Questions
Mathc the type of packing given in Column I with the itmes given in Column II.
Column -I
(i) square close packing in two dimensions
(ii) Hexagonal close packing in two dimensions
(iii) Hexagonal close packing in three dimensions
(iv) Cubic close packing in three dimensions
Column -II (a) Triagnular voids
(b) Pattern of spheres is reapted in every fourth layer
(c) Coordination number -4
(d) Pattern of sphere is reapeated i alternate layers.
View SolutionMatch the type of packing given in column I with the iterms given in column II.
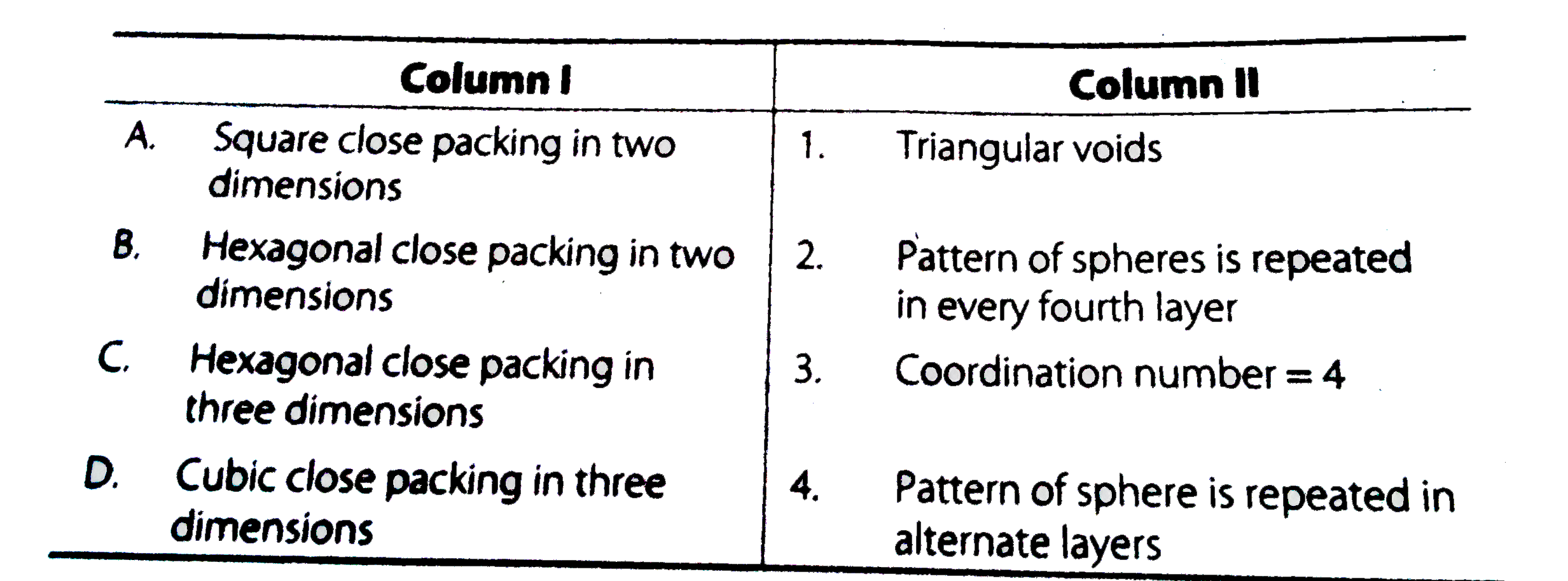
View Solution
Knowledge Check
Packing refers to the arrangement of constituent units in such a way that the forces of attraction among the constituent particles is the maximum and the contituents occupy the maximum available space. In two dimensions, there are hexagonal close packing and cubic close packing. In three dimentions, there are hexagonal, cubic as well as body centred close packings.
The empty space left in hcp packing is:A26%B74%C52.4%D80%Packing refers to the arrangement of constituent units in such a way that the forces of attraction among the constituent particles is the maximum and the contituents occupy the maximum available space. In two dimensions, there are hexagonal close packing and cubic close packing. In three dimentions, there are hexagonal, cubic as well as body centred close packings.
The space occupied by spheres in bcc arrangement is:A74%B70%C68%D60.4%Packing refers to the arrangement of constituent units in such a way that the forces of attraction among the constituent particles is the maximum and the contituents occupy the maximum available space. In two dimensions, there are hexagonal close packing and cubic close packing. In three dimentions, there are hexagonal, cubic as well as body centred close packings.
The pattern of successive layers in ccp arrangement is:AABABAB…BABABC ABABC…CABCABCABC…DAB BA AB BA…
Packing refers to the arrangement of constituent units in such a way that the forces of attraction among the constituent particles is the maximum and the contituents occupy the maximum available space. In two dimensions, there are hexagonal close packing and cubic close packing. In three dimentions, there are hexagonal, cubic as well as body centred close packings.
The empty space left in ccp packing is:
View SolutionPacking refers to the arrangement of constituent units in such a way that the forces of attraction among the constituent particles is maximum and the constituents occupy the maximum available space. In two -dimensions ,there are square close packing and hexagonal close packing .In three- dimensions ,however, there are hexagonal close packing, cubic close packing and body-centered cubic packing.
(i) hcp: AB AB AB AB ..... arrangement
coordination no. = 12
% occupied space = 74
(ii) ccp: ABC ABC.... arrangement lt brgt coordination no. = 12
% occupied space = 74
bcc: 68% space is occupied
coordination no.= 8
The empty space laft in three -dimensions is :
View SolutionPacking refers to the arrangement of constituent units in such a way that the forces of attraction among the constituent particles is maximum and the constituents occupy the maximum available space. In two -dimensions ,there are square close packing and hexagonal close packing .In three- dimensions ,however, there are hexagonal close packing, cubic close packing and body-centered cubic packing.
(i) hcp: AB AB AB AB ..... arrangement
coordination no. = 12
% occupied space = 74
(ii) ccp: ABC ABC.... arrangement lt brgt coordination no. = 12
% occupied space = 74
bcc: 68% space is occupied
coordination no.= 8
The closed packed lattice containing 'n' particles ,the numbers of tetrahedral and octahedral voids are:
View SolutionThree-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
The coordination number of cubic closed packing is:
View SolutionThree-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
The correct statement about zns crystal is:
View Solution
