Let OAB be a quadrant of a circle with boundary radii and bunding arc AB. Then
Maximum area of the reactangle inscribed in it with two vertices on OA and OB and two on the are AB
A
B
C
D
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - III (Straight Objective Type Question)
62 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - IV (Straight Objective Type Question)
38 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - II(Matrix Matching Type Questions)
5 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
Knowledge Check
In the circle given below . Let OA = 1 unit , OB = 13 unit and PQ ⊥ OB. Then the area of the triangle PQB ( in square units)is
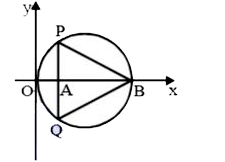 A24√2B24√3C26√3D26√2
A24√2B24√3C26√3D26√2AB is a straight line and O is a point on AB, if a line OC is drawn not coinciding with OA or OB, then ∠AOC and ∠BOC are
AequalBcomplementaryCsupplementaryDtogether equal to 100AB is a straight line and O is a point on AB, if a line OC is drawn not coinciding with OA or OB, then ∠AOC and ∠BOC are
AequalBcomplementaryCsupplementaryDtogether equal to 100
P is a point on a circle with centre 0. If P is equidistant from the two radii OA and OB, prove that arc AP=arcBP.
View SolutionIn an isoceles triangle OAB , O is the origin and OA=OB=6 . The equation of the side AB is x-y+1=0 Then the area of the triangle is
View SolutionIn an isoceles triangle OAB , O is the origin and OA=OB=6 . The equation of the side AB is x-y+1=0 Then the area of the triangle is
View SolutionThe radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
View SolutionLet AOB be the positive quadrant of the ellipse x2a2+y2b2=1 with OA=a , OB=b .
Then show that the area bounded between the chord AB and the arc AB of the ellipse is (π−2)ab4
View Solution