In an Isosceles triangle ABC taken on the Base AC is a point M such that AM = a MC = b. Circles are described in the triangles ABM and CBM then distance between points at which these circles touch the side BM is
|a−b|
|a−b|2
|a−b|3
√ab
The correct Answer is:B
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL II) (LECTURE SHEET (ADVANCED)) (More than one correct answer Type Questions)
19 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL II) (LECTURE SHEET (ADVANCED)) (Matrix Matching Type Questions)
9 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE SHEET (EXERCISE-IV) (LEVEL-II) (Matrix Matching Type Questions)
2 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
If an isosceles triangle ABC , in which AB = AC = 10 cm , is inscribed in a circle of radius 10 cm , find the area of the triangle .
View SolutionIf an isosceles triangle ABC in which AB=AC=6cm is inscribed in a circle of radius 9cm, find the area of the triangle.
View SolutionTwo circles are drawn with sides AB and AC of a triangle ABC as diameters
View SolutionInscribed in a circles is an isosceles triangle ABC whose base AC=b and the base angle is α. A second circle touches the first circle and the base of the triangle at its midpoint D, and is situated outside the triangle. Find the radius of the second circle.
View SolutionIn the figure, all three sides of a triangle ABC touch the circle at points P, Q and R. Find the value of x.
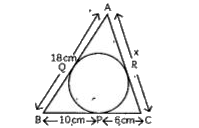
View SolutionA circle touches the triangle ΔABC at side BC at point P and touches at Q and R if AB and AC are extended. If perimeter of the triangle is 16 cm then find the length from A to Q.

View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides AB and AC at D and E respectively. Prove that DEBC
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DECB.
View SolutionIn ΔABC,M is the mid point of BC. Length of AM is 9, N is a point on AM such that MN=1. What is the distance of N from the centroid of the triangle?
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View Solution
