∠PBC, ∠QBC, ∠RBC are three isosceles triangles on the same base BC. Show that P, Q, R are collinear.Solution in Assamese
Step by step video & image solution for /_PBC, /_QBC, /_RBC are three isosceles triangles on the same base BC. Show that P, Q, R are collinear. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - KALYANI PUBLICATIONCHAPTER - GEOMETRYEXERCISE - EXERCISE
10 Videos
- GEOMETRICAL CONSTRUCTIONBOOK - KALYANI PUBLICATIONCHAPTER - GEOMETRICAL CONSTRUCTIONEXERCISE - EXERCISE
3 Videos
- HARDER PRODUCT AND FACTORISATION BOOK - KALYANI PUBLICATIONCHAPTER - HARDER PRODUCT AND FACTORISATION EXERCISE - EXERCISE
148 Videos
Similar Questions
l is the perpendicular bisector of the line segment PQ and R is a point on the some side of l as P. The line segment QR intersects l at X. Prove that PX+XR=QR.
View SolutionConstruct a triangle ABC such that BC=6 cm AB =6 cm and median AD=5 cm
View SolutionIn the formula,
a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)
if a+b+c=0, then show that
a3+b3+c3=3abc
View SolutionDelta ABC and Delta DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए चित्र) | यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करें, तो दर्शाइए कि

AP रेखाखंड BC का लम्ब समद्विभाजक है |
View Solutionদেখাও যে, (p, q,r), (q,r, p) এবং (r, p,q) বিন্দু তিনটির সংযোগে একটি সমবাহু ত্রিভুজ উৎপন্ন হয়।
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
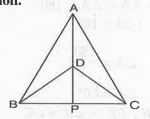 ).If AD is extended to intersect BC at P, show that ΔABD≅ΔACD.
).If AD is extended to intersect BC at P, show that ΔABD≅ΔACD.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
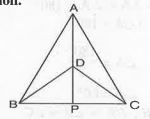 ).If AD is extended to intersect BC at P, show that ΔABP≅ΔACP.
).If AD is extended to intersect BC at P, show that ΔABP≅ΔACP.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
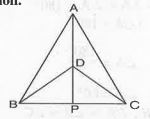 ).If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D.
).If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
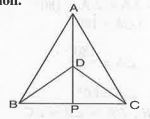 ).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.
).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.
View SolutionThe base vertices of an isosceles triangle PQR are Q=(1,3) and R=(−2,7). The vertex P can be
View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
ΔABP≅ΔACP
View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
AP bisects angle BAC and BDC.
View Solution
