If 2x+1x−2≤1,x∈R , then the solution set is
(−∞,12)
(−∞,−12]
[−3,2]
[−3,2)
The correct Answer is:D
To solve the inequality 2x+1x−2≤1, we will follow these steps:
Step 1: Rewrite the Inequality
We start with the inequality:
2x+1x−2≤1
Step 2: Move All Terms to One Side
We can subtract 1 from both sides:
2x+1x−2−1≤0
Step 3: Combine the Fractions
To combine the fractions, we need a common denominator:
2x+1−(x−2)x−2≤0
This simplifies to:
2x+1−x+2x−2≤0
x+3x−2≤0
Step 4: Find Critical Points
Now, we need to find the critical points where the expression is equal to zero or undefined. The critical points are:
1. x+3=0⇒x=−3
2. x−2=0⇒x=2 (undefined)
Step 5: Test Intervals
We will test the intervals determined by the critical points −3 and 2:
- Interval 1: (−∞,−3)
- Interval 2: (−3,2)
- Interval 3: (2,∞)
Testing Interval 1: x=−4
−4+3−4−2=−1−6>0(not a solution)
Testing Interval 2: x=0
0+30−2=3−2<0(solution)
Testing Interval 3: x=3
3+33−2=61>0(not a solution)
Step 6: Include Critical Points
The inequality is less than or equal to zero, so we include the point where the expression equals zero:
- At x=−3, −3+3−3−2=0 (included)
- At x=2, the expression is undefined (not included)
Final Solution Set
Thus, the solution set is:
x∈(−3,2)
Summary
The final answer is:
Solution set: (−3,2)
We start with the inequality:
2x+1x−2≤1
We can subtract 1 from both sides:
2x+1x−2−1≤0
To combine the fractions, we need a common denominator:
2x+1−(x−2)x−2≤0
This simplifies to:
2x+1−x+2x−2≤0
x+3x−2≤0
Now, we need to find the critical points where the expression is equal to zero or undefined. The critical points are:
1. x+3=0⇒x=−3
2. x−2=0⇒x=2 (undefined)
We will test the intervals determined by the critical points −3 and 2:
- Interval 1: (−∞,−3)
- Interval 2: (−3,2)
- Interval 3: (2,∞)
−4+3−4−2=−1−6>0(not a solution)
0+30−2=3−2<0(solution)
3+33−2=61>0(not a solution)
The inequality is less than or equal to zero, so we include the point where the expression equals zero:
- At x=−3, −3+3−3−2=0 (included)
- At x=2, the expression is undefined (not included)
Thus, the solution set is:
x∈(−3,2)
The final answer is:
Solution set: (−3,2)
Topper's Solved these Questions
- BOOK - ICSECHAPTER - LINEAR INEQUALITIES EXERCISE - MULTIPLE CHOICE QUESTION16videos
LINEAR INEQUALITIES
- BOOK - ICSECHAPTER - LIMITS AND DERIVATIVES EXERCISE - Multiple Choice Questions31videos
LIMITS AND DERIVATIVES
- BOOK - ICSECHAPTER - MATHEMATICAL INDUCTIONEXERCISE - Exercise (a)1videos
MATHEMATICAL INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
If x2−5≤x3−4,x∈R, then the solution set of x on the number line is:
A B
B C
C D
D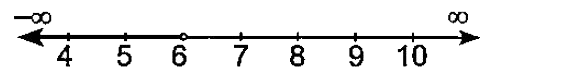
- Question 2 - Select One
If 1x−1≥2 , then the solution set is
AA. (1,32]BB. [1,32]CC. (1,32)DD. (−∞,−3]∪[12,∞) - Question 3 - Select One
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A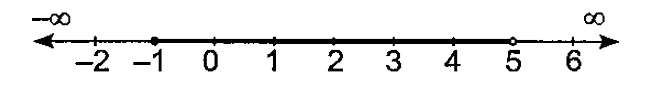 B
B C
C D
D
Find the values of x, which satisfy the inequation: −2≤12−2x3<156,x∈N Graph the solution set on the real number line.
View SolutionIf 2≤2x−3≤5,x∈I, then the solution set of x on the number line is:
View SolutionIf 2x−3<x+1<4x+7,x∈R then the solution set of x on the number line is:
View SolutionIf 2x−3≤x+1≤4x+7,x∈I (integers), then the solution set of x is
View SolutionIf −1<3+4x≤23,x∈R (real numbers), then the solution set of x is
View Solution

