A mathematical pendulum 1 m long is deflected from the vertical by an angle of 40∘ and let go. Find the period of oscillations using numerical methods.
What will be the error, if in this case we use the formula for small oscillations?
The correct Answer is:2.08
The particle.s velocity at an arbitrary point on the circle is Fig
v−√2gh=√2gl(cosα−cosα0)=√2gl
where x=√cosα−cosα0. The body travels along the element of arc Δs=lΔα in time
Δl=Δsvnv=lΔαxav√2gl=Δαxn√2√lg
Put Δα=3∘=π/60 radian. Then
Δt=2π√1g.√2240xav
The period of oscillations is
T=4(Δt1+Δt2+......)=2π√lg√260(1x1av+1x2av+)

Since the formula T0=2π√l/g is used to compute the period of small oscillations, it follows that T=kT0, where
k=√260(1x1av+1x2av+.........)
is the correction factor. Let us compile a table from the computed data. We have
k=√2×44.2360=1.042
Hence, the period T=2πk√l/g=2.08 s, the value of T0 being T02π√l/g=2.00 s. In this case the relative error due to the use of the formula for small oscillations will be 4%.
समान प्रश्न
দোলকের দৈর্ঘ্য l ও দোলনকাল T যদি T= 2π(√lg) সূত্র দ্বারা আবদ্ধ হয় এবং দৈর্ঘ্যের ত্রুটি 1% হলে দোলনকালের ত্রুটি নির্ণয় করো
View Solutionएक लोलक का द्रव्यमान 1 किग्रा है तथा उसकी प्रभावी लम्बाई 10 मी है
(a) कम आयाम के दोलनों के लिए लोलक का आवर्तकाल ज्ञात कीजिए
(b) यदि दोलन का कोणीय आयाम 60∘ हो तो आवर्तकाल कितना होगा ?
View SolutionA hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum . How does it differ from the time period calculated using the formula for a simple pendulum?
View SolutionA hollow sphere of radius 2 cm is attached to an 18 cm long thread to made a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
View SolutionA mathematical pendulum 1 m long is deflected from the vertical by an angle of 40^(@) and let go. Find the period of oscillations using numerical methods. What will be the error, if in this case we use the formula for small oscillations?
View Solutionएक पेंडुलम 60∘ के कोण पर दोलन करता है और 8.8 cm लम्बा चाप बनाता है। पेंडुलम की लंबाई ज्ञात कीजिए (π=227 का प्रयोग करें।)
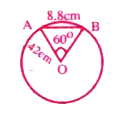
View SolutionThe pendulum in a clock is 14 ~cm long. It moves through 40^(circ) makes one oscillation. What is the distance travelled by the tip of the pendulum during one oscillation?
View Solution
