A circle touches all the four sides of a quadrilateral . Prove that: .
BC + DA = AB + CD
ABCD is a rectangle
ABCD is square
None of these
The correct Answer is:A
Step by step video, text & image solution for A circle touches all the four sides of a quadrilateral A B C D . Prove that: A B+C D=B C+D A . by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If any quadrilateral ABCD, prove that sin(A+B)+sin(C+D)=0 cos(A+B)=cos(C+D)
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
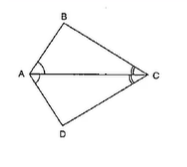
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIf A,B,C,D are the four angles taken in order of a cyclic quadrilateral prove that tan A+tan B+tan C+tan D=0
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionIf A, B, C, D are angles of a cyclic quadrilateral, prove that cosA+cosB+cosC+cosD=0.
View SolutionCalculate the area of the quadrilateral ABCD as shown in Fig.33, given that BD=42 cm , AC=28 cm , OD=12 cm and AC⊥BD .
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionIf A,B,C,D are angles of a cyclic quadrilateral, then prove that cosA+cosB+cosC+cosD=0
View Solution
