Circles C(o, r) and C(O1,r2) touch internally at a point A and AB is a chord of the circle intersecting C(O1,r2) at C. Then AC is equal to :
CB
OA
OB
13 AB
The correct Answer is:A
Step by step video, text & image solution for Circles C(o, r) and C(O^(1), (r)/(2)) touch internally at a point A and AB is a chord of the circle intersecting C(O^(1), (r)/(2)) at C. Then AC is equal to : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
In Figure, circle C(O,r)andC(O′r2) touch internally at a point. AandAB is a chord of the circle C(O,r) intersecting C(O′,r2) at C . Prove that AC=CB
View SolutionCircles C(O, r) and C(O', r'), (r>r') touch internally at P. PQ is a chord of circle C(O, r) which intersects C(O', r') at R. Show that OO'RQ is a trapezium
View Solution
Knowledge Check
- Question 1 - Select One
IF two circles of radii r1 and r2 (r2>r1) touch internally , then the distance between their centres will be
Ar1−r2Br2−r1Cr21−r22Dr22−r21
If O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionAB is the common tangent to the circles C1 and C2. C1 and C2 are touching externally at C.AD and DC are two chords of the circle C1 and BE and CE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC
View SolutionIn the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
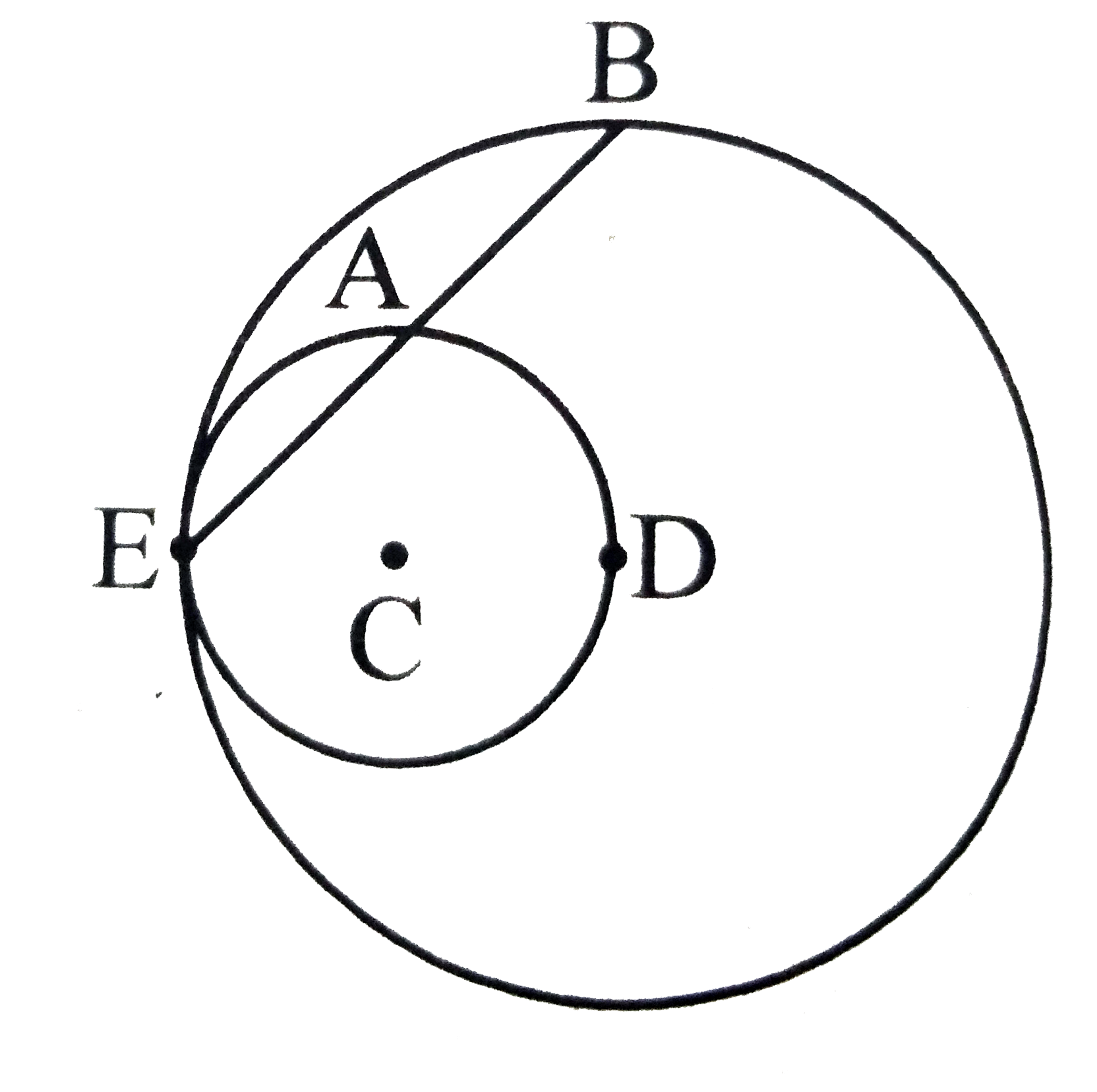 View Solution
View SolutionTwo circles with centres O1andO2 touch each other externally at a point R. AB is a tangent to both the circles passing through R. P'Q' is an-other tangent to the circles touching them at P and Q respectively and also cutting AB at S. PQ measures 6 cm and the point S is at distance of 5 cms and 4 cms from the centres of the circles. What is the area of triangle SO1O2?
View SolutionIn the following figure, (not a scale), AB is the common tangent to the circles C1andC2 and C1andC−2 are touching externally at C. AD and DC are two chords of the circle, C1andBEandCE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC.
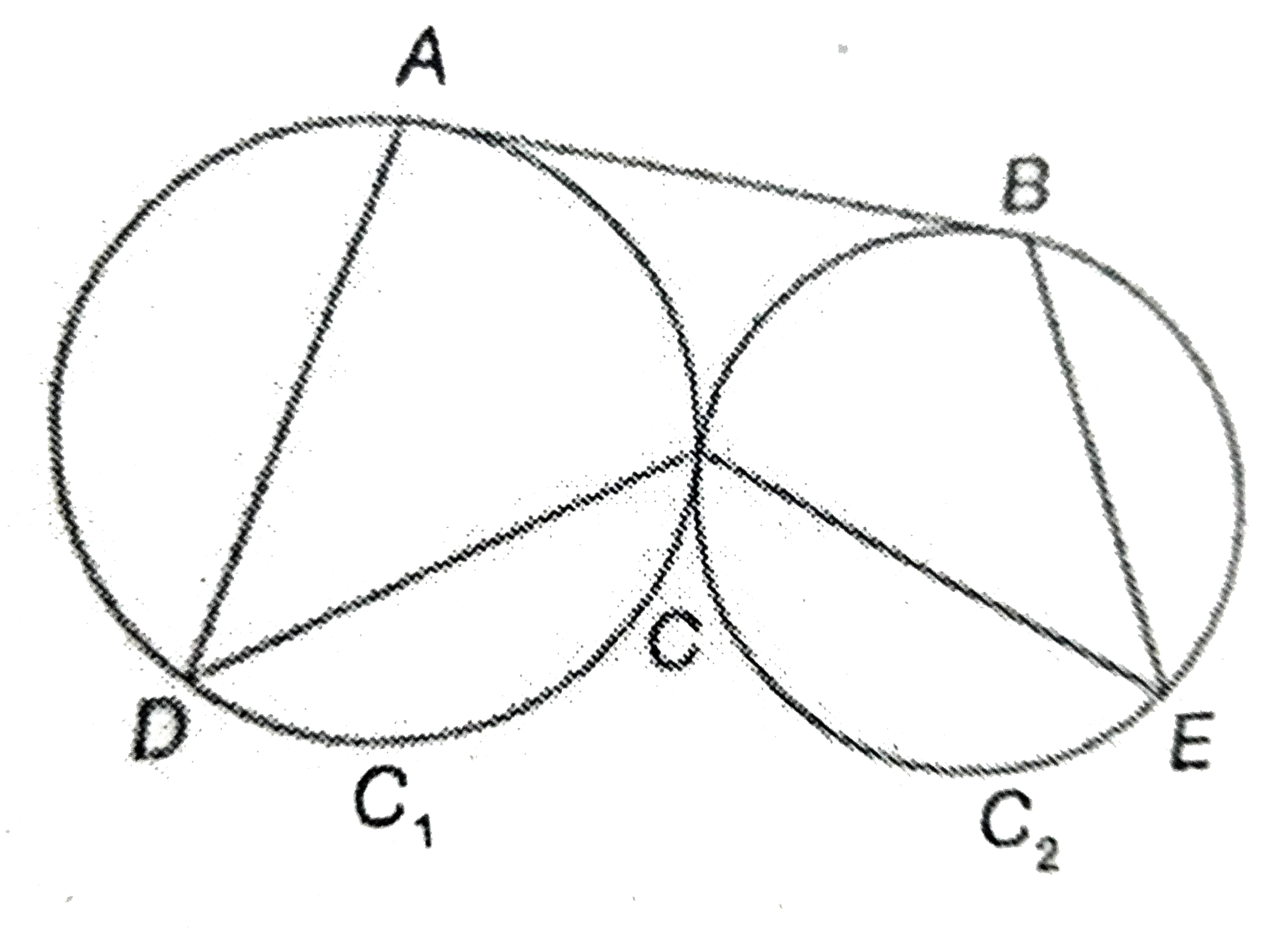 View Solution
View SolutionIn the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
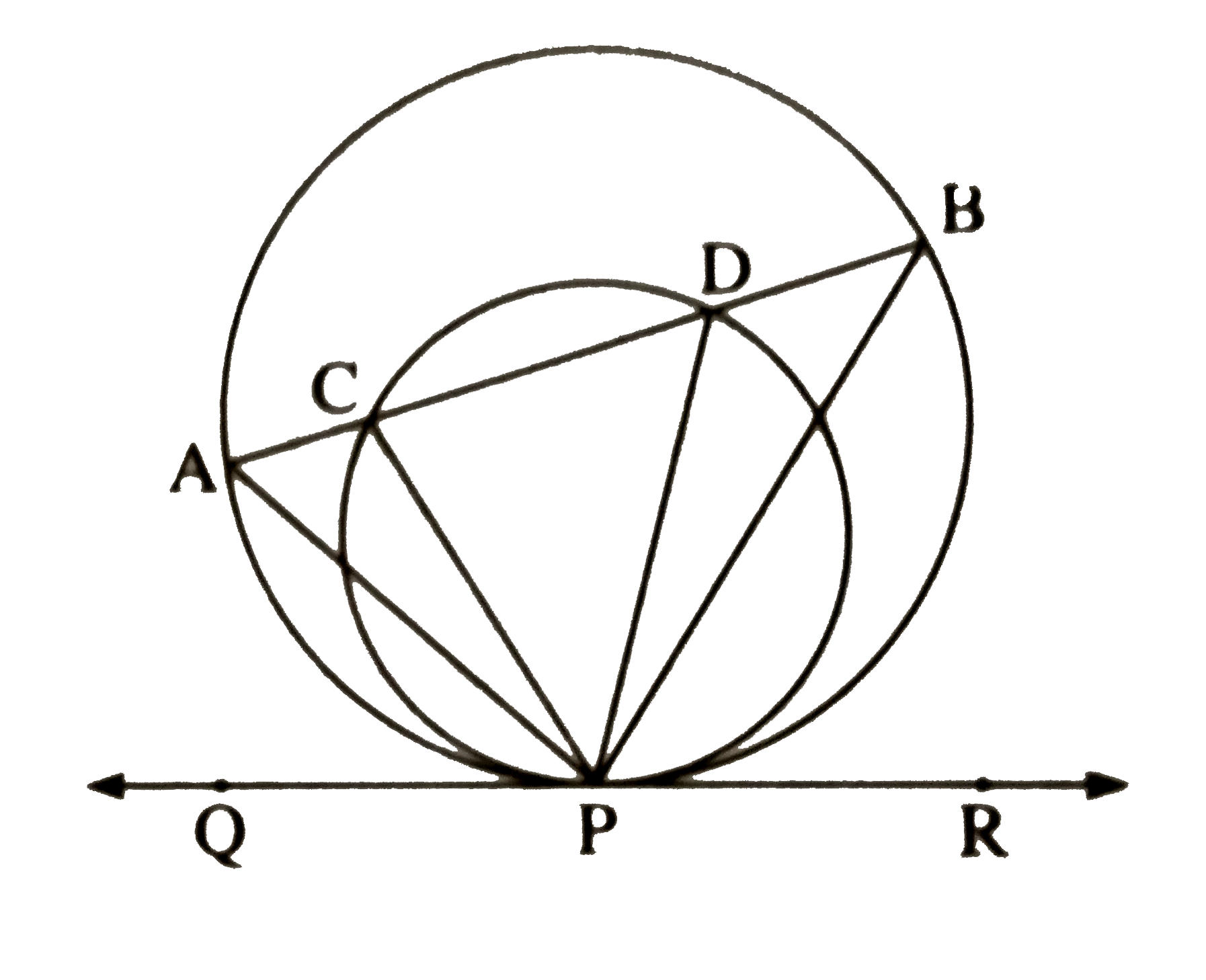 View Solution
View SolutionTwo circles C(0, r) and C(O', r') touch extemally. Show that the length of a common tangent (not through the point of contact of the circles) is 2√rr'
View Solution

