In two Concentric circles, AB and CD are two chords of the outer circle which touch the inner circle at E and F. Then :
AB = CD
AB=12CD
AB≠CD
None of these
The correct Answer is:A
To solve the problem involving two concentric circles with chords AB and CD that touch the inner circle at points E and F respectively, we can follow these steps:
1. Understand the Setup:
- We have two concentric circles, meaning they share the same center. Let’s denote the center as O.
- Chord AB of the outer circle touches the inner circle at point E.
- Chord CD of the outer circle touches the inner circle at point F.
Hint: Visualize the two circles and label the center and the points where the chords touch the inner circle.
2. Identify the Properties of Chords:
- Since AB touches the inner circle at E, the distance from the center O to the chord AB is equal to the radius of the inner circle at point E.
- Similarly, since CD touches the inner circle at F, the distance from O to the chord CD is equal to the radius of the inner circle at point F.
Hint: Remember that the distance from the center to a chord is the same as the radius of the inner circle at the point of tangency.
3. Use the Equidistance Property:
- The distances OE (from O to E) and OF (from O to F) are equal because both points E and F lie on the inner circle.
- Therefore, the distances from the center O to the chords AB and CD are equal.
Hint: Think about how the radii of a circle are always equal.
4. Conclude About the Chords:
- Since the distances from the center O to both chords AB and CD are equal, it follows that the lengths of the chords AB and CD must also be equal.
- Thus, we can conclude that AB = CD.
Hint: Reflect on the relationship between the distance from the center to the chords and the lengths of the chords themselves.
Final Conclusion:
The lengths of the chords AB and CD are equal because they are both equidistant from the center of the concentric circles.
- We have two concentric circles, meaning they share the same center. Let’s denote the center as O.
- Chord AB of the outer circle touches the inner circle at point E.
- Chord CD of the outer circle touches the inner circle at point F.
- Since AB touches the inner circle at E, the distance from the center O to the chord AB is equal to the radius of the inner circle at point E.
- Similarly, since CD touches the inner circle at F, the distance from O to the chord CD is equal to the radius of the inner circle at point F.
- The distances OE (from O to E) and OF (from O to F) are equal because both points E and F lie on the inner circle.
- Therefore, the distances from the center O to the chords AB and CD are equal.
- Since the distances from the center O to both chords AB and CD are equal, it follows that the lengths of the chords AB and CD must also be equal.
- Thus, we can conclude that AB = CD.
The lengths of the chords AB and CD are equal because they are both equidistant from the center of the concentric circles.
Topper's Solved these Questions
Similar Questions
In two concentric circles prove that all chords of the outer circle which touch the inner circle are of equal length.
View SolutionFind the area of the region between the two concentric circles, if the length of a chord of the outer circle just touching the inner circle at a particular point on it is 10 cm (Take, π=227)
View Solution
Knowledge Check
Two concentric circle of radii 3cm and 5cm are given. Find the chord BC which touches the inner circle at P.
 A5cmB8cmC9cmDNone
A5cmB8cmC9cmDNoneTwo concentric circles having common centre O and chord AB of the outer circle intersect the inner circle at points C and D. If distance of chord from the centre is 3 cm, outer radius is 13 cm inner radius is 7 cm, then length of AC (in cm) is
A8√10B6√10C4√10D2√10In a college, the ratio of the number of boys to girls is 8 : 5. If there are 160 girls, the total number of students in the college is
AA) 100BB) 250CC) 260DD) 416
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact.
View SolutionThere are two concentric circles with centre O and a chord AB of outer circle cut the inner circle at C and D. If distance of chord to centre is 3 cm, outer radius is 13 cm and inner radius is 7 cm, then length of AC is-
View SolutionThe radii of two co-centric circles are 13 cm and 8 cm respectively. AB is diameter of outer circle and BE is tangent to the inner circles which touches the inner circle at point D. Then find the length of AD.
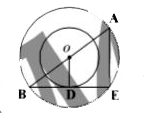
View SolutionIn the figure , two concentric circles of radii a&b(a>b) are given.The chord AB of larger circle touches the smaller circle at C .The length AB is :
View SolutionProve that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
View Solution
