CD is direct common tangent to two circles intersecting each other at A and B. The ∠CAD+∠CBD is equal to

180∘
90∘
360∘
120∘
The correct Answer is:A
Step by step video & image solution for CD is direct common tangent to two circles intersecting each other at A and B. The angle CAD + angle CBD is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
CD is direct common tangent to two circles intersecting each other at A and B. The ∠CAD+∠CBD is equal to
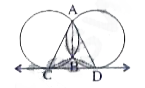 A120∘B90∘C360∘D180∘
A120∘B90∘C360∘D180∘O is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘and∠APB=30∘, then tan2∠APB+cot2∠COD is equal to :
A43B103C13D23Two circles of radii 8 cm and 2 cm respectively touch each other externally at the point A. PQ is the direct common tangent of these two circles of centres O1andO2 respectively. The length of PQ is equal to :
A4 cmB8 cmC2 cmD3 cm
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If ∠AOB=15∘and∠APB=30∘, then ∠COD is equal to
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.

View SolutionProve that if two lines intersect each other, then the vertically opposite angles are equal.
View SolutionIf two lines intersect each other, then the vertically opposite angles are equal.
View Solution

