C is a point on the minor arc AB of the circle with centre O. Given ∠ACB=x∘and∠AOB=y∘. Calculate x, if ACBO is a parallelogram.
120∘
180∘
140∘
110∘
The correct Answer is:A
To solve the problem, we need to analyze the properties of the angles in the circle and the parallelogram formed by points A, B, C, and O.
1. Understanding the Parallelogram:
In a parallelogram, opposite angles are equal. Therefore, in parallelogram ACBO, we have:
∠ACB=∠AOB
2. Using the Inscribed Angle Theorem:
The inscribed angle theorem states that the angle subtended by an arc at the center of the circle is twice the angle subtended at any point on the circumference. Thus, we have:
∠AOB=2×∠ACB
This means:
y=2x
where y is the angle AOB and x is the angle ACB.
3. Setting Up the Equation:
From the relationship we established, we can express x in terms of y:
x=y2
4. Final Calculation:
If we know the value of y (angle AOB), we can directly calculate x using the equation derived above. If y is not given, we cannot find a numerical value for x without additional information.
Conclusion:
Thus, the angle x can be calculated as:
x=y2
In a parallelogram, opposite angles are equal. Therefore, in parallelogram ACBO, we have:
∠ACB=∠AOB
The inscribed angle theorem states that the angle subtended by an arc at the center of the circle is twice the angle subtended at any point on the circumference. Thus, we have:
∠AOB=2×∠ACB
This means:
y=2x
where y is the angle AOB and x is the angle ACB.
From the relationship we established, we can express x in terms of y:
x=y2
If we know the value of y (angle AOB), we can directly calculate x using the equation derived above. If y is not given, we cannot find a numerical value for x without additional information.
Thus, the angle x can be calculated as:
x=y2
Topper's Solved these Questions
Similar Questions
Knowledge Check
C is a point on the minor arc AB a circle with centre O. If ∠AOB=100∘, what is ∠ACB ?
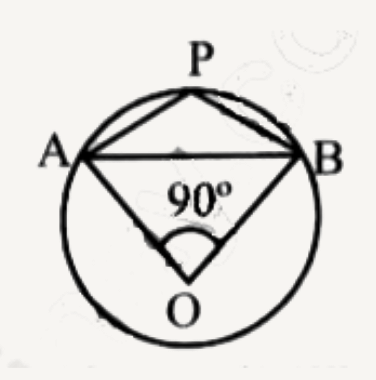
A80∘B90∘C100∘D130∘O is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to
 A150∘B210∘C75∘D105∘
A150∘B210∘C75∘D105∘∠ACB is inscribed in arc ACB of a circle with centre O . If ∠ACB=65∘ , find m ( arc ACB ) .
A65∘B130∘C295∘D230∘
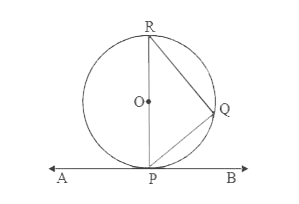
In the given figure, O is the centre of the circle, ∠AOB=90∘. Find ∠APB :
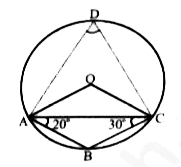
View SolutionIn the figure, O is centre of a circle. If ∠BAC=20∘and∠ACB=30∘. Find ∠AOC
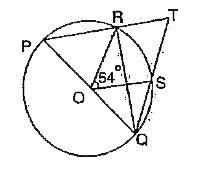
View SolutionPQ is the diameter of the given circle, whose centre is O. Given, ∠Ros=54∘, calculate ∠RTS.
View SolutionAnswer True or False. ACB is an arc of a circle with centre O and ∠ABC=45∘, then, AO⊥OC.
View SolutionIn the figure , O is the centre and ∠ACB=20∘∠AOD is equal to

View Solution