Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
65
130
195
135
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Given Information
We have two circles with centers P and Q that intersect at points B and C. Points A and D lie on the circles with centers P and Q respectively, and points A, C, and D are collinear. We know that ∠APB=130∘ and we need to find ∠BQD=x∘.
Step 2: Draw the Diagram
Draw two intersecting circles with centers P and Q. Mark the points of intersection as B and C. Place point A on the circle centered at P and point D on the circle centered at Q, ensuring that points A, C, and D are collinear.
Step 3: Use the Inscribed Angle Theorem
According to the Inscribed Angle Theorem, the angle at the center of the circle is twice the angle at the circumference subtended by the same arc.
Let ∠APB=130∘. The angle subtended by arc AB at point C (which we will call ∠ACB) will be half of ∠APB:
∠ACB=12×∠APB=12×130∘=65∘
Step 4: Identify the Cyclic Quadrilateral
Since points A, B, C, and D form a cyclic quadrilateral (as they lie on the circumference of the circles), we can use the property that the sum of the opposite angles in a cyclic quadrilateral is 180∘.
Let ∠ACB=65∘ and let ∠ADB=z. According to the cyclic quadrilateral property:
∠ACB+∠ADB=180∘
Thus,
65∘+z=180∘
From this, we can find z:
z=180∘−65∘=115∘
Step 5: Find the Angle at the Center Q
Now, we will find ∠BQD. Since ∠BQD is the angle at the center Q subtended by the same arc BD, we can use the same theorem again.
Let ∠BQD=x. The angle at the circumference (which is ∠ADB=z) is:
x=2×z=2×115∘=230∘
Step 6: Final Calculation
However, since angles in a circle must be less than 360∘, we need to adjust our angle x:
x=230∘−180∘=50∘
Conclusion
Thus, the value of x is 50∘.
We have two circles with centers P and Q that intersect at points B and C. Points A and D lie on the circles with centers P and Q respectively, and points A, C, and D are collinear. We know that ∠APB=130∘ and we need to find ∠BQD=x∘.
Draw two intersecting circles with centers P and Q. Mark the points of intersection as B and C. Place point A on the circle centered at P and point D on the circle centered at Q, ensuring that points A, C, and D are collinear.
According to the Inscribed Angle Theorem, the angle at the center of the circle is twice the angle at the circumference subtended by the same arc.
∠ACB=12×∠APB=12×130∘=65∘
Since points A, B, C, and D form a cyclic quadrilateral (as they lie on the circumference of the circles), we can use the property that the sum of the opposite angles in a cyclic quadrilateral is 180∘.
∠ACB+∠ADB=180∘
Thus,
65∘+z=180∘
From this, we can find z:
z=180∘−65∘=115∘
Now, we will find ∠BQD. Since ∠BQD is the angle at the center Q subtended by the same arc BD, we can use the same theorem again.
x=2×z=2×115∘=230∘
However, since angles in a circle must be less than 360∘, we need to adjust our angle x:
x=230∘−180∘=50∘
Thus, the value of x is 50∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135 - Question 2 - Select One
If 76 is divided into four parts proportional to 7, 5, 3, 4, then the smallest part is:
AA) 12BB) 15CB) 15DD) 19 - Question 3 - Select One
Alloy A contains 40% gold and 60% silver. Alloy B contains 35% gold and 40% silver and 25% copper. Alloys A and B are mixed in the ratio of 1:4 .What is the ratio of gold and silver in the newly formed alloy is?
AA) 20% and 30%BB) 36% and 44%CC) 25% and 35%DD) 49% and 36%
Two circles whose centres are O and O' intersect at P. Through P, a line l parallel to OO' intersecting the circles at C and D is drawn. Prove that CD=2 OO'
View SolutionThe tangents at two points A and B on the circle with centre O intersect at P. If in quadrilateral PAOB, ∠AOB:∠APB=5:1, then measure of ∠APB is :
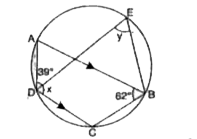
View SolutionIn the diagram, A, B, C, D, E are points on the circle. AB||DC, ∠ADE=39∘and∠ABC=62∘. Then the values of x and y respectively are :
 View Solution
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘and∠APB=30∘, then tan2∠APB+cot2∠COD is equal to :
View SolutionA, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 110°∘and 130∘ respectively. Then the value of ∠BAC is :
View Solution