A, B, C are three point on a circle. The tangent at A meets BC produced at T, . The angle subtended by BC at the centre of the circle is -
The correct Answer is:D
To solve the problem, we need to find the angle subtended by chord BC at the center of the circle, given the angles at point T where the tangent at point A meets line BC produced.
1. Identify Given Angles:
- Angle BTA=40∘
- Angle CAT=44∘
2. Find Angle ACT:
- Since T is a point on the tangent and A is a point on the circle, we can use the property of angles in a triangle.
- The angle ACT can be found using the fact that the sum of angles in triangle ACT is 180∘.
- Therefore,
ACT=180∘−(BTA+CAT)=180∘−(40∘+44∘)=180∘−84∘=96∘
3. Find Angle ACB:
- Angle ACB is the angle subtended by chord BC at point A.
- Angle ACB is equal to angle CAT because they are in the same segment of the circle.
- Thus,
ACB=CAT=44∘
4. Find Angle BAC:
- To find angle BAC, we can use the triangle ABC.
- The sum of angles in triangle ABC gives:
BAC+ACB+ABC=180∘
- We already know ACB=44∘ and ABC=40∘ (since ABC is equal to BTA).
- Therefore,
BAC+44∘+40∘=180∘
BAC+84∘=180∘
BAC=180∘−84∘=96∘
5. Find Angle at the Center:
- The angle subtended by chord BC at the center of the circle is twice the angle subtended at any point on the circumference.
- Therefore, the angle subtended by BC at the center O is:
Angle at center=2×BAC=2×96∘=192∘
Final Answer:
The angle subtended by chord BC at the center of the circle is 192∘.
---
- Angle BTA=40∘
- Angle CAT=44∘
- Since T is a point on the tangent and A is a point on the circle, we can use the property of angles in a triangle.
- The angle ACT can be found using the fact that the sum of angles in triangle ACT is 180∘.
- Therefore,
ACT=180∘−(BTA+CAT)=180∘−(40∘+44∘)=180∘−84∘=96∘
- Angle ACB is the angle subtended by chord BC at point A.
- Angle ACB is equal to angle CAT because they are in the same segment of the circle.
- Thus,
ACB=CAT=44∘
- To find angle BAC, we can use the triangle ABC.
- The sum of angles in triangle ABC gives:
BAC+ACB+ABC=180∘
- We already know ACB=44∘ and ABC=40∘ (since ABC is equal to BTA).
- Therefore,
BAC+44∘+40∘=180∘
BAC+84∘=180∘
BAC=180∘−84∘=96∘
- The angle subtended by chord BC at the center of the circle is twice the angle subtended at any point on the circumference.
- Therefore, the angle subtended by BC at the center O is:
Angle at center=2×BAC=2×96∘=192∘
The angle subtended by chord BC at the center of the circle is 192∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A, B and C are three points on a circle. The tangent at C meets BA extended at T. Given, ∠ATC=36∘and∠ACT=48∘, the angle subtended by AB at the centre of the circle is
A84∘B48∘C96∘D72∘ - Question 2 - Select One
A, B and C are the three points on a circle such that ∠ABC=35∘and∠BAC=85∘. What is the angle (in degrees) subtended by arc AB at the centre of the circle?
A60B90C135D120 - Question 3 - Select One
A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If ∠ATC=30∘ and ∠ACT=48∘, then what is the value of ∠AOB?
A78∘B96∘C102∘D108∘
The total plane angle subtended by a circle at its centre is
View SolutionIn figure , BOA is a diameter of circle and the tangent at point P meets BA produced at. T if ∠PBO=30∘ then ∠PTA=
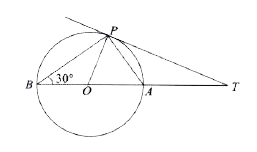 View Solution
View SolutionAB is a diameter of a circle with centre O. The tangents at C meets AB produced at Q. if ∠CAB=34∘, then measure of is ∠CBA is
View SolutionThe angle subtended by the diameter at any point on the circles is a/an_______angle.
View SolutionAB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?View Solution

