The bisector of interior ∠Aof△ABC meets BC in D, and the bisector of exterior angle ∠Ameets BC produced in E. prove that BDBE=CDCE
CECD
CDCE
ADAE
AEAD
The correct Answer is:B
Step by step video, text & image solution for The bisector of interior angleA of triangleABC meets BC in D, and the bisector of exterior angle angleA meets BC produced in E. prove that (BD)/(BE)= (CD)/(CE) by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The bisector of ∠A of ΔABC cuts BC at D and the circumcircle of the triangle at E. then
AAB:AC=BD:DCBAD:AC=AE:ABCAB:AD=AC:AEDAB:AB=AE:AC - Question 2 - Select One
The bisector of the exterior ∠A of ΔABC intersects the side BC produced to D. Here CF is parallel to AD.
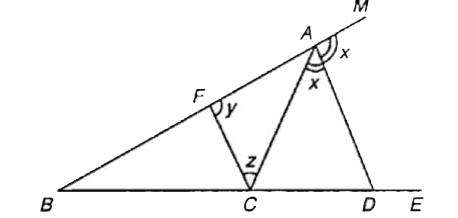 AABAC=BDCDBABAC=CDBDCABAC=BCCDDnone of these
AABAC=BDCDBABAC=CDBDCABAC=BCCDDnone of these
If the bisector of the angle A of triangle ABC meets BC in D, prove that a=(b+c)[1−[AD]2bc]12
View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionAD is a median of △ABC. The bisectors of ∠ADBand∠ADC meets AB and AC in E and F respectively prove that EF||BC.
View SolutionIn a triangle ABC, the bisector of angle A meets the opposite side at D. Using vectors prove that BD:DC=c:b.
View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionThe bisector of ∠A in △ABC meets BC in D. If AB = 15 cm, AC = 13 cm and BC = 14 cm, then DC =?
View Solution

