In a circle, a diameter AB and a chord PQ (which is not a diameter) intersect each other at X perpen- dicularly. If AX : BX = 3:2 and the radius of the circle is 5 cm, then the length of chord PQ is:
2√13 cm
5√3 cm
4√6 cm
6√5 cm
To find the length of the chord PQ in the given circle, we will follow these steps:
Step 1: Understand the given information
We have a circle with diameter AB and a chord PQ that intersects AB at point X perpendicularly. We are given the ratio AX : BX = 3 : 2 and the radius of the circle is 5 cm.
Step 2: Calculate the length of diameter AB
Since the radius of the circle is 5 cm, the diameter AB can be calculated as:
AB=2×radius=2×5=10 cm
Step 3: Set up the equation for AX and BX
Let AX = 3k and BX = 2k, where k is a common multiplier. According to the information given:
AX+BX=AB⟹3k+2k=10
5k=10⟹k=2
Step 4: Calculate AX and BX
Now we can find the lengths of AX and BX:
AX=3k=3×2=6 cm
BX=2k=2×2=4 cm
Step 5: Determine the position of point O (center of the circle)
Since AB is the diameter, the center O of the circle is the midpoint of AB. Therefore:
AO=OB=AB2=102=5 cm
Step 6: Calculate OX
Since AX = 6 cm, we can find OX:
OX=AO−AX=5−6=−1 cm(This indicates that point X is 1 cm below point O)
Thus, the distance OX is actually 1 cm (the absolute value).
Step 7: Use Pythagorean theorem to find QX
Now we will use the Pythagorean theorem in triangle OXQ:
QO2=QX2+OX2
Where QO is the radius of the circle (5 cm) and OX is 1 cm:
52=QX2+12
25=QX2+1⟹QX2=25−1=24
QX=√24=2√6 cm
Step 8: Calculate the length of chord PQ
Since PX = QX (because X is the midpoint of PQ),
PQ=PX+QX=2QX=2×2√6=4√6 cm
Final Answer
The length of chord PQ is 4√6 cm.
---
We have a circle with diameter AB and a chord PQ that intersects AB at point X perpendicularly. We are given the ratio AX : BX = 3 : 2 and the radius of the circle is 5 cm.
Since the radius of the circle is 5 cm, the diameter AB can be calculated as:
AB=2×radius=2×5=10 cm
Let AX = 3k and BX = 2k, where k is a common multiplier. According to the information given:
AX+BX=AB⟹3k+2k=10
5k=10⟹k=2
Now we can find the lengths of AX and BX:
AX=3k=3×2=6 cm
BX=2k=2×2=4 cm
Since AB is the diameter, the center O of the circle is the midpoint of AB. Therefore:
AO=OB=AB2=102=5 cm
Since AX = 6 cm, we can find OX:
OX=AO−AX=5−6=−1 cm(This indicates that point X is 1 cm below point O)
Thus, the distance OX is actually 1 cm (the absolute value).
Now we will use the Pythagorean theorem in triangle OXQ:
QO2=QX2+OX2
Where QO is the radius of the circle (5 cm) and OX is 1 cm:
52=QX2+12
25=QX2+1⟹QX2=25−1=24
QX=√24=2√6 cm
Since PX = QX (because X is the midpoint of PQ),
PQ=PX+QX=2QX=2×2√6=4√6 cm
The length of chord PQ is 4√6 cm.
Topper's Solved these Questions
Similar Questions
In a circle of radius 3 units, a diameter AB intersects a chord of length 2 units perpendicularly at P. If AP>BP, then what is the ratio of AP to BP?
View SolutionIn a circle of radius 2 units, a diameter AB intersects a chord of length 2 units perpendicularly at P. If AP>BP, then AP is equal to
View Solution
Knowledge Check
In a circle, a diameter AB and a chord PQ (which is not a diameter) intersect each other at X perpendicularly. If AX : BX = 3 : 2 and the radius of the circle is 5 cm, then the length of chord PQ is
A2√13 cmB2√13 cmC4√6 cmD6√5 cmIn a circle, a diameter AB and a chord PQ (which is not a diameter) intersect each other at X perpen- dicularly. If AX : BX = 3:2 and the radius of the circle is 5 cm, then the length of chord PQ is:
A2√13cm.B5√3cm.C4√6cm.D6√5cm.O is the centre of a circle. AB is a chord of the circle but not its diameter. OC is perpendicular to AB. If OC = CB and radius of the circle be 7 cm, then the length of AB is
A7√2cmB14cmC7 cmD7√2 cm
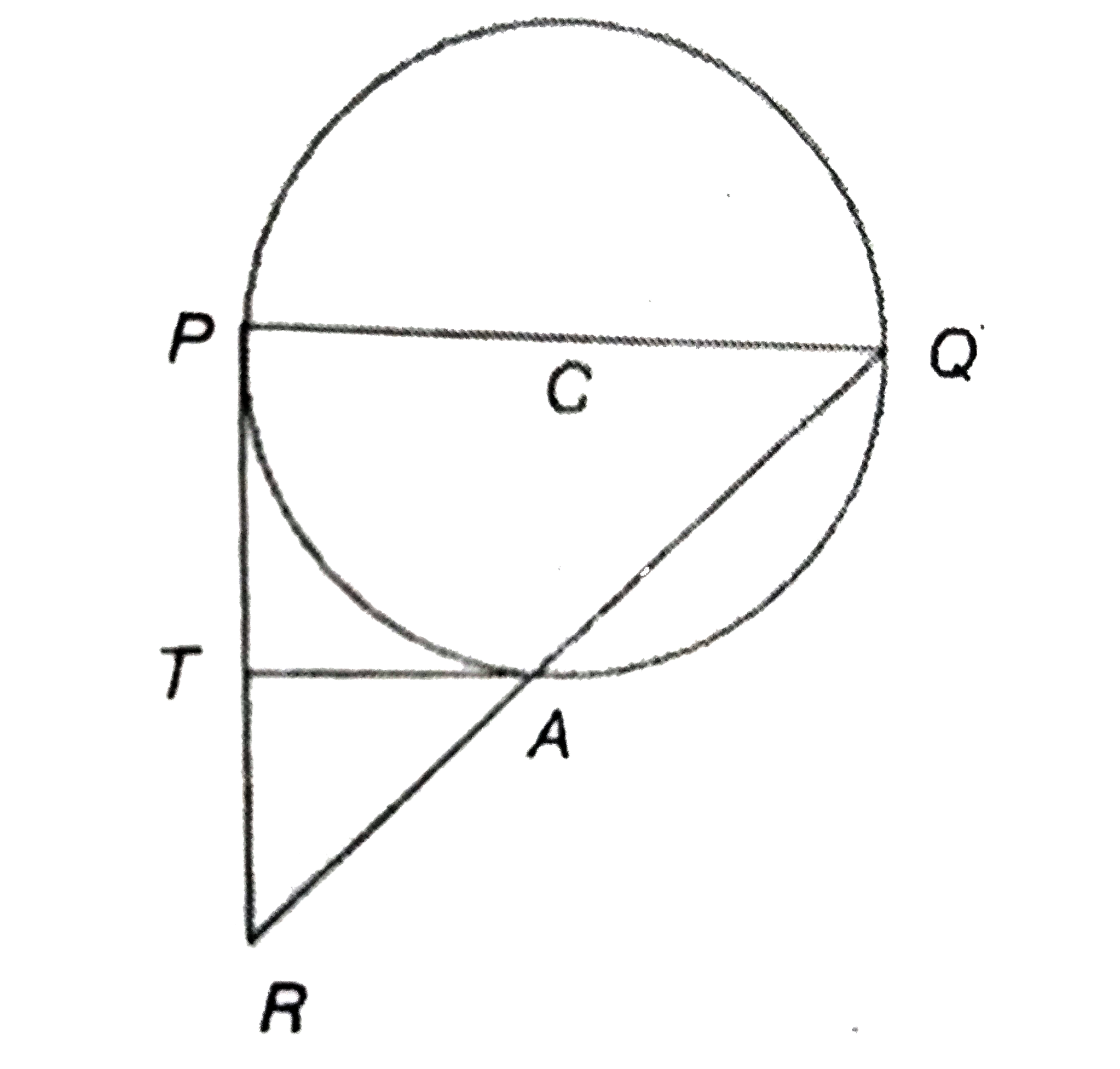
In the following figure,PQ is the diameter of the circle with radius 5 cm. if AT is the tangent and equal to the radius of the circle, then find the lenth of AR.
View SolutionTwo circles of radii 7cm and 5 cm intersect each other at A and B, the distance between their centres is 10 cm. The length (in cm) of the common chord AB is:
दो वृत्त, जिनकी त्रिज्याएँ 7 सेमी तथा 5 सेमी हैं, एक-दूसरे को A और B पर प्रतिच्छेद करते हैं | उनके केंद्रों के बीच की दूरी 10 सेमी है | उभयनिष्ठ जीवा AB की लंबाई ( सेमी में ) कितनी है ?
View SolutionIn a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
View SolutionIn a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
View SolutionIn a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is:
View Solution
