A and B are the centers of two circles with radii 11 cm and 6 cm respectively. A common tangent touches these circles at P and Q respectively. If AB = 13 cm, then the length of PQ is:
13 cm
17 cm
8.5 cm
12 cm
To find the length of the common tangent PQ between the two circles with centers A and B, we can use the formula for the length of the common tangent between two circles:
PQ=√AB2−(R1−R2)2
where:
- AB is the distance between the centers of the circles,
- R1 is the radius of the first circle,
- R2 is the radius of the second circle.
1. Identify the given values:
- The distance between the centers AB=13cm
- The radius of the first circle R1=11cm
- The radius of the second circle R2=6cm
2. Calculate the difference in radii:
R1−R2=11−6=5cm
3. Substitute the values into the formula:
PQ=√AB2−(R1−R2)2
PQ=√132−52
4. Calculate AB2 and (R1−R2)2:
132=169
52=25
5. Subtract the squares:
PQ=√169−25
PQ=√144
6. Take the square root:
PQ=12cm
Final Answer:
The length of PQ is 12cm.
- AB is the distance between the centers of the circles,
- R1 is the radius of the first circle,
- R2 is the radius of the second circle.
- The distance between the centers AB=13cm
- The radius of the first circle R1=11cm
- The radius of the second circle R2=6cm
R1−R2=11−6=5cm
PQ=√AB2−(R1−R2)2
PQ=√132−52
132=169
52=25
PQ=√169−25
PQ=√144
PQ=12cm
The length of PQ is 12cm.
Topper's Solved these Questions
Similar Questions
A and B are centres of two circles whose radii are 5 cm and 2 cm respectively. The direct common tangent meets the extended AB point P. The P divides the AB-
View SolutionThe side AB, BC and CA of triangle ABC touch a circle at P,Q and R respectively. If PA =4 cm, BP=3 cm and AC=11 cm, then length of BC is

View Solution
Knowledge Check
A and B are centres of the two circles whose radii are 5 cm and 2 cm respectively. The direct common tangents to the circles meet AB extended at P.Then p divides AB
Ainternally in the ratio 5:2Binternally in the ratio 2:5Cexternally in the ratio 5:2Dexternally in the ratio 7:2Two circles touch each other externally at point A and PQ is a direct tangent which touch circle at P and Q respectively then ∠PAQ = ?
A45∘B90∘C80∘D100∘If two circles with radii 5 cm and 3 cm respectively touch externally, then the distance between their centre is ________
A2cmB4cmC8cmD16cm
If two circles with radii 5 cm and 3 cm respectively touch internally, find the distance between their centres.
View SolutionTwo circles with radius 4 cm and 9 cm respectively touch each other externally. Their common tangent touches the circles at point P and Point Q respectively. Then, area of the square with side PQ is.
View SolutionIf two circles with radii 8 cm and 3 cm respectively touch externally, then find the distance between their centres.
View SolutionIn the figure, the circles with centeres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD, if the radii of the circle are 4 cm, 6 cm.
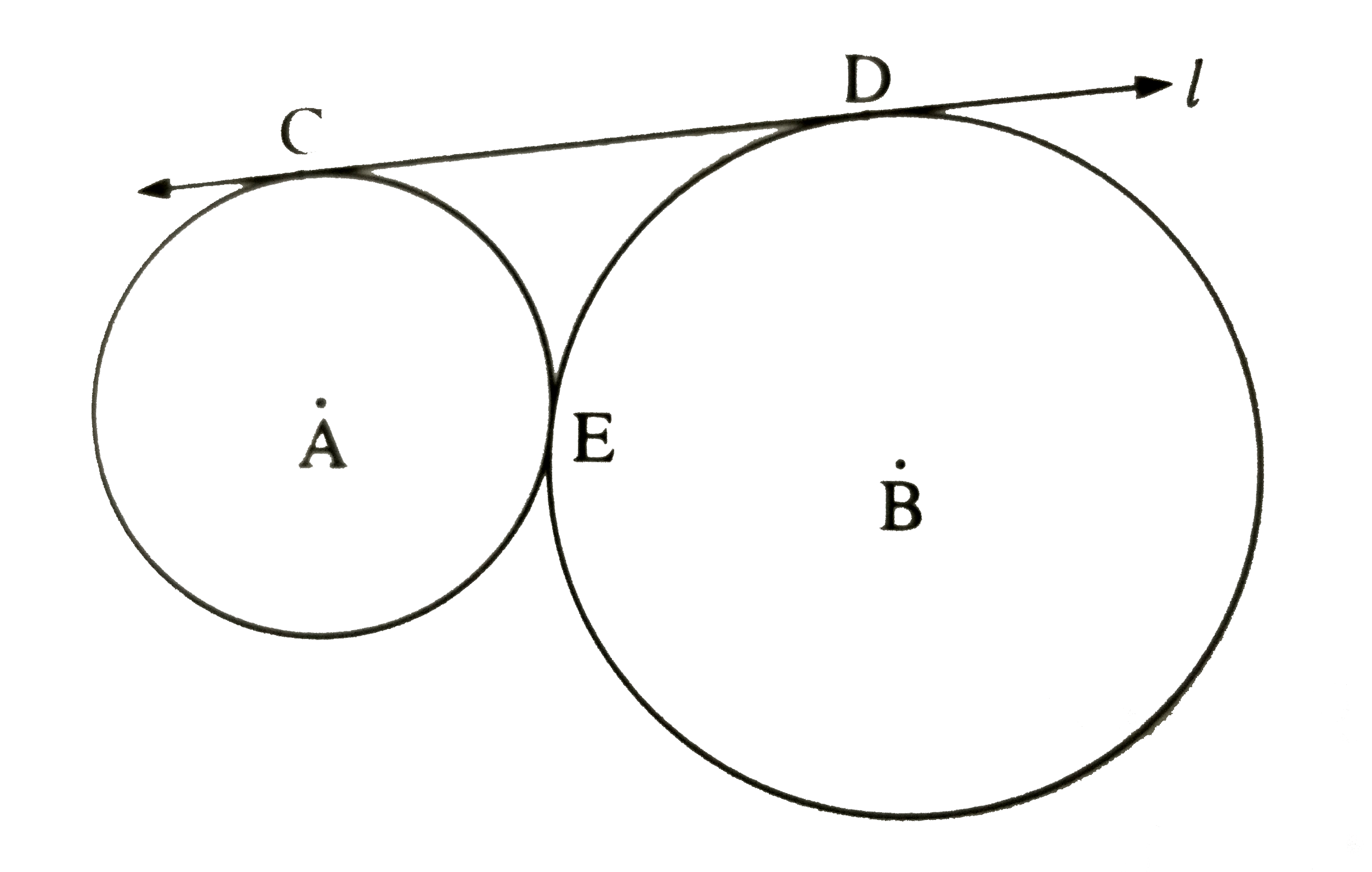
View SolutionTwo same circles of radius 5 cm has a direct tangent AB and a transversal CD which touch circle at A, B and C, D respectively. If CD = 24 cm then find the length of AB (in cm)?
View Solution
