Solve Problem 25.7 assuming that the plates remain connected to the voltage source.
In this case, too, the capacitance of the capacitor increases as the liquid rises, but the energy of the electric field is not conserved but increases. Besides, the potential energy of the rising water increases as well. Is this not in contradiction with the law of conservation of energy? Of course not. The power supply performs work to raise the liquid, the increase in the energy of the system being equal to the work of the power supply in displacing the charges to the capacitor plates:
Wp.s=ΔWel+Δpot
But Wp.s=Δq.φ=(C−C0)φ2
Substituting, we obtain the result sought after some simple transformations.
Similar Questions
Knowledge Check
Consider a parallel plate capcaitor with plates 20 cm by 20 cm and separated by 2 mm. The dielectric constant of the material between the plates is 5. The plates are connected to a voltage source of 500 V. The energy density of the field between the plates will be close to
A2.65J/m3B1.95J/m3C1.38J/m3D0.69J/m3Consider a parallel plate capcaitor with plates 20 cm by 20 cm and separated by 2 mm. The dielectric constant of the material between the plates is 5. The plates are connected to a voltage source of 500 V. The energy density of the field between the plates will be close to
A2.65J/m3B1.95J/m3C1.38J/m3D0.69J/m3
The distance between the plates of a plane capacitor is 10 mm, the voltage is 10 kV. A sheet of mica of the same dimensions as those of the plates is then inserted between the plates. Find the polarization charge on the surface of the mica sheet assuming the plates to remain connected to the power supply.
View SolutionThe distance between the plates of a plane capacitor is 10 mm, the voltage is 10 kV. A sheet of mica of the same dimensions as those of the plates is then inserted between the plates. Find the polarization charge on the surface of the mica sheet assuming the plates to remain connected to the power supply.
View SolutionA large vessel is filled with a liquid. Two vertical plates touch the surlace of the liquid (Fig. 25.7). The dimensions of the plates are a and b, the distance between them is d. The plates have been charged by applying a voltage Po and then disconnected from the voltage source. To what height will the liquid rise? Ignore capillary effects.
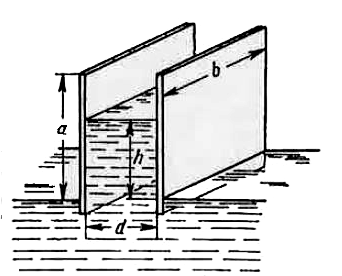
View SolutionA large vessel is filled with a liquid. Two vertical plates touch the surlace of the liquid (Fig. 25.7). The dimensions of the plates are a and b, the distance between them is d. The plates have been charged by applying a voltage Po and then disconnected from the voltage source. To what height will the liquid rise? Ignore capillary effects.

View SolutionSolve Problem 25.1 assuming the capacitor to have been initially charged and subsequently disconnected before the mica sheet is inserted in it.
View SolutionSolve Problem 25.1 assuming the capacitor to have been initially charged and subsequently disconnected before the mica sheet is inserted in it.
View Solution
