The wire star of the previous problem is connected to the circuit at points P and C. Find the equivalent resistance.
The correct Answer is:r
The problem may be solved in stages. First we replace the star connection by an equivalent resistance shown in Fig. 26.4a, and then by an equivalent resistance shown in Fig. 26.4b. It is evident from considerations of symmetry that the potentials of points H and K are equal and so the connection HK may be removed. We obtain a circuit whose resistance is easily found to be a half of the resistance of either of the two parallel links of three conductors.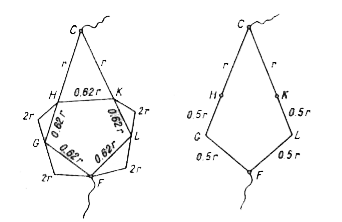 
Similar Questions
suppose the ends of the coil in the previous problem are connected to a resistane of 100Ω. Neglecting the resistance of the coil, find the heat produced in the circuit in one minute.
View Solutionsuppose the ends of the coil in the previous problem are connected to a resistane of 100Ω. Neglecting the resistance of the coil, find the heat produced in the circuit in one minute.
View Solution
Knowledge Check
- Question 1 - Select One
The equivalent resistance of the circuit across points A and B is equal to
A22.5ΩB25ΩC37.5ΩD75Ω - Question 2 - Select One
The equivalent resistance of the given circuit between points A and B is :
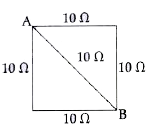A40ΩB4ΩC5ΩD0.2Ω
A cube is soldered together írom identical pieces of wire each of a resistance r. It is connected to the circuit at the corners lying on opposite ends of a body diagonal Find the equivalent resistance.
View SolutionA cube is soldered together írom identical pieces of wire each of a resistance r. It is connected to the circuit at the corners lying on opposite ends of a body diagonal Find the equivalent resistance.
View SolutionWhat will be the motion of the conductor of the previous problem, if a resistor of resistance R is connected into the circuit instead of the capacitor? Neglect the resistance of the conductors.
View SolutionWhat will be the motion of the conductor of the previous problem, if a resistor of resistance R is connected into the circuit instead of the capacitor? Neglect the resistance of the conductors.
View SolutionThe equivalent resistance of the circuit across points A and B is equal to
View SolutionFind the equivalent resistance of the circuit between the points A and B
View Solution