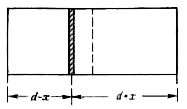
A piston of mass m divides a cylinder containing gas into two equal parts. Suppose the piston is displaced to the left to a distance x and let go Fig. Assuming the process to take place at a constant temperature, find the frequency of the piston's oscillations.
The correct Answer is:ωiost0=√2pV/md2
When the volume of a gas is changed at constant temperature we have, according to the Boyle-Maniotte Jaw
p1(d−x)S=p2(d+x)S=pdS
The force acting on the pistion is
F=(p1−p2)S=2pxSdd2−x2=2pVxd2−x2
where V is the volume of one half of the vessel. As can be seen, the force does not conform to Hooke.s law, and the oscillations are not harmonic. But for small deflections of the piston (when x<<d ), the force will be quasi-elastic: F=2pVx/d2 and the oscillations of the piston will be harmonic. The rigidity of the system isk=F/x=2pV/d2.
Similar Questions
A heat conducting piston can move freely inside a closed thermally isolated cylinder which contains an ideal gas. In equilibrium the piston divides the cylinder in two equal parts, the temperature of the gas being T0. The piston is slowly displaced. Find the temperature of the gas when the volume of one part is n times greater than that of the other part. The adiabatic exponent of the gas is γ.
View SolutionA heat conducting piston can move freely inside a closed, thermally insulated cylinder with an ideal gas (γ= 5/3). At equilibrium, the piston divides the cylinder into two equal parts, the gas temperature being equal to 300 K. The piston is slowly displaced by an external agent. Find the gas temperature when the volume of the greater section is seven times the volume of the smaller section.
View Solution
Knowledge Check
- Question 1 - Select One
A cylinder piston of mass M sides smoothly inside a long cylinder closed at and enclosing a certain mass of gas The cylinder is kept with its axis horizontal if the piston is distanced from its equations positions it oscillation simple harmonically .The period of oscillation will be
 AT=2π√(MhPA)BT=2π√(MAPb)CT=2π√(MPAh)DT=2π√MPhA
AT=2π√(MhPA)BT=2π√(MAPb)CT=2π√(MPAh)DT=2π√MPhA - Question 2 - Select One
An ideal gas is enclosed in a vertical cylindrical container and supports a freely moving piston of mass M. The piston and the cylinder have an equal cross-sectional area A. Atmospheric pressure is p0 and when the piston is in equilibrium, the volume of the gas is V0. The piston is now displaced slightly from its equilibrium position. Assuming that the system, is completely isolated from, its surroundings, what is the frequency of oscillation.
Af=12π√γ(p0A2+MgA)V0MBf=12π√1γ(p0A2+MgA)V0MCf=12π√(p0A2+MgA)V0MDf=12π√A(p0A2+MgA)V0M - Question 3 - Select One
An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A12π√MV0AγP0B12πAγP0V0MC12πV0MP0A2γD12π√A2γP0MV0
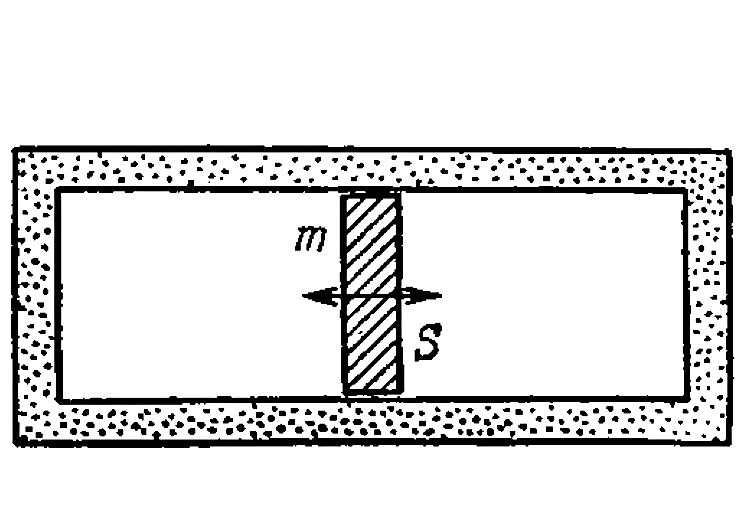
In a cylinder filled up with ideal gas end gas and closed from both ends there is a piston of mass m and cross − sectional area S (figure).In equilibrium the piston divides the cylinder into two equal parts, each with volime V0 . The gas ppressure is p0. The piston was slightly displaced from the equlibrium position and released.Find the oscillation frequency, assuming the prosecces in the gas to be adiabatic and the friction negligible.
 View Solution
View SolutionA weightless piston divides a thermally insulated cylinder into two equal parts. One part contains one mole of an ideal gas with adiabatic exponent γ, the other is evacuated. The initial gas temperature is T0. The piston is released and the gas fills the whole volume of the cylinder. Then the piston is slowly displaced back to the initial position. Find the increment of the internal energy and entropy of the gas was resulting from these two processes.
View SolutionA heat-conducting piston can freely move inside a closed thermally insulated cylinder with an ideal gas. In equilibrium the piston divides the cylinder into two equal parts, the gas temperature being equal to T0. The piston is slowly displaced. Find the gas temperature as a function of the ratio η of the volumes of the greater and smaller sections. The adiabatic exponent of the gas is equal to γ.
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View Solution

