The period of a simple pendulum for large deflection angles may be determined from the approximate formula
T=2π√lg(1+14sin2α02)
Compare with the result of numerical calculations for the previous problem.
The correct Answer is:ε=1%
Similar Questions
Knowledge Check
The periodic time (T) of a simple pendulum of length (L) is given by T=2π√Lg. What is the dimensional formula of T√gL?
A[M0L1T0]B[M0L0T0]C[M1L1T−1]D[M0L−1T1]If the time period of a simple pendulum is T=2π√l/g , then the fractional error in acceleration due to gravity is
A4π2ΔlΔT2BΔll−2ΔlTCΔll+2ΔTTDNone of theseThe l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
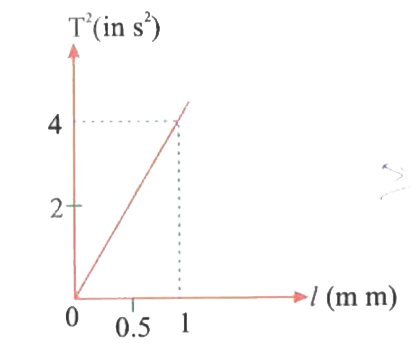 A1sB1.2 sC√2 sD1√2s
A1sB1.2 sC√2 sD1√2s
Assertion : If the length of the simple pendulum is equal to the radius of the earth, the period of the pendulum is T=2π√R/g
Reason : Length of this pendulum is equal to radius of earth.
View SolutionTime period T of a simple pendulum of length l is given by T =2π√lg . If the length is increased by 2% then an approximate change in the time period is
View SolutionThe time period of a simple pendulum is 4 s and the acceleration due to gravity at the given place is 9.8ms−2 . Write the following steps in sequential order to find the length of the pendulum.
(A) From the above formula, write the value of l and l=T2.g4π2
(B) Note the given values of the time period (T) and acceleration due to gravity (g).
(C)Write the formula, T=2π√lg , where l is the length of the pendulum.
(D). Substitute the given data and get the value of l.
View SolutionWhile determining the value of g using simple pendulum, we plot a graph between l and T2 which is
View SolutionIn the previous problem if t is the time period of rotation
(i) t=2π√Lg
(ii) t=2π√Lcosθg
(iii) T=4π2mLt2
(iv) The ball is in equilibrium
View Solution
