A freely body acquires a velocity of gxhy after falling through a height h. Using dimensions find the values fo x and y.
To solve the problem of finding the values of x and y in the expression for velocity v=gxhy where g is the acceleration due to gravity and h is the height, we will use dimensional analysis.
Step 1: Write down the dimensions of the quantities involved.
- The dimension of velocity v is (v)=LT−1.
- The dimension of acceleration due to gravity g is (g)=LT−2.
- The dimension of height h is (h)=L.
Step 2: Express the dimensions of the right-hand side.
The expression for velocity in terms of g and h is given by:
v=gxhy
Substituting the dimensions:
(v)=(g)x(h)y
This translates to:
LT−1=(LT−2)x(L)y
Simplifying the right-hand side:
LT−1=Lx+yT−2x
Step 3: Equate the dimensions on both sides.
From the equation LT−1=Lx+yT−2x, we can separate the dimensions of L and T:
1. For the dimensions of L:
1=x+y(1)
2. For the dimensions of T:
−1=−2x(2)
Step 4: Solve the equations.
From equation (2):
−1=−2x⟹x=12
Substituting x=12 into equation (1):
1=12+y⟹y=1−12=12
Conclusion:
The values of x and y are:
x=12,y=12
Thus, the expression for velocity can be written as:
v=g12h12=√gh
- The dimension of velocity v is (v)=LT−1.
- The dimension of acceleration due to gravity g is (g)=LT−2.
- The dimension of height h is (h)=L.
The expression for velocity in terms of g and h is given by:
v=gxhy
Substituting the dimensions:
(v)=(g)x(h)y
This translates to:
LT−1=(LT−2)x(L)y
Simplifying the right-hand side:
LT−1=Lx+yT−2x
From the equation LT−1=Lx+yT−2x, we can separate the dimensions of L and T:
1. For the dimensions of L:
1=x+y(1)
2. For the dimensions of T:
−1=−2x(2)
From equation (2):
−1=−2x⟹x=12
1=12+y⟹y=1−12=12
The values of x and y are:
x=12,y=12
Thus, the expression for velocity can be written as:
v=g12h12=√gh
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS10videos
DIMENSIONS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - LONG ANSWER QUESTIONS3videos
DIMENSIONS
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS50videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS12videos
DYNAMICS
Similar Questions
If (x+y, x-y) = (3, 1), find the values of x and y.
View SolutionA body freely falling from the rest has velocity v after it falls through a height h the distance it has to fall down for its velocity to become double is
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
 View Solution
View SolutionA ball of mass m strikes the fixed inclined plane after falling through a height h. if it rebounds elastically. The impulse on the ball is :
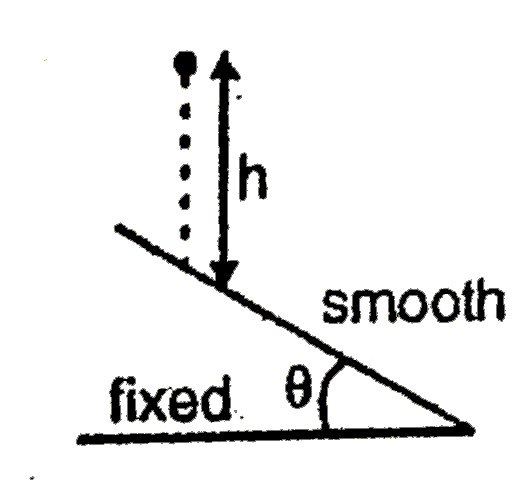 View Solution
View SolutionA body of mass m falls down through a height h. Obtain an expression for the work done by the force of gravity
View SolutionA small drop of water falls from rest through a large height h in air, the final velocity is
View SolutionIn the adjoining figure, find x,y and h.
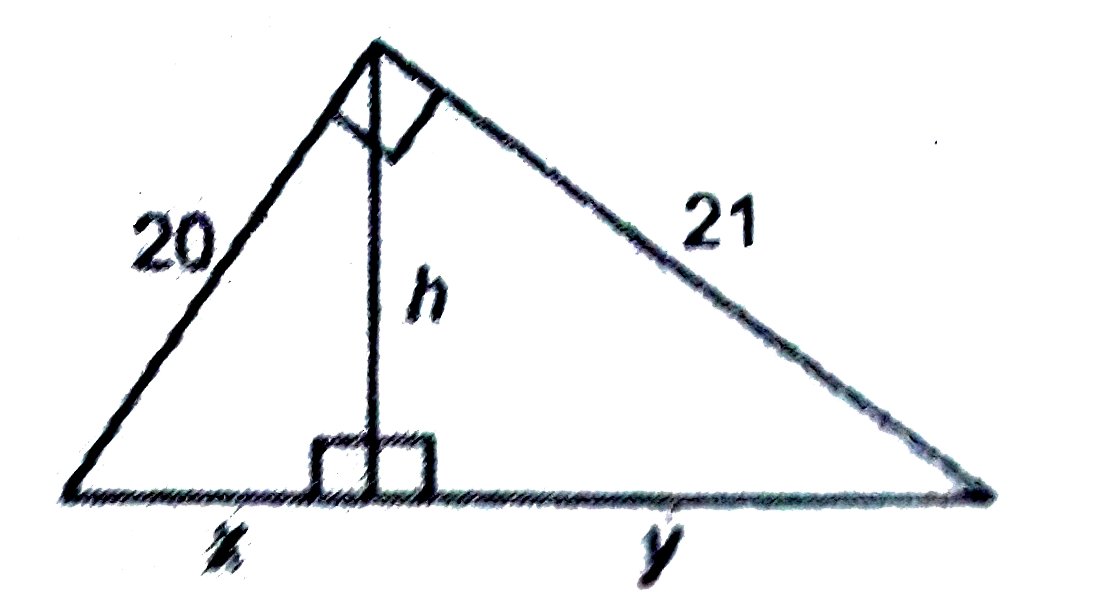 View Solution
View SolutionP=nxyTV0e−MghnxT, where n is number of moles, P is represents acceleration due to gravity and h is height. Find dimension of x and value of y.
View SolutionThe velocity of a freely falling body changes as gphqwhere g is acceleration due to gravity and h is the height. The values of p and q are
View SolutionA solid sphere rolls down a parabolic path , whose vertical dimension is given by y=kx2 and base of the parabola is at x = 0 . During the fall the sphere does not slip, but beyond the base the climb is frictionless. If the sphere falls through a height h, the height above the base that it would climb is
View Solution

