P=nxyTV0e−MghnxT, where n is number of moles, P is represents acceleration due to gravity and h is height. Find dimension of x and value of y.
The correct Answer is:[ML2T−2μ−1K−1][M0L−0T0]
To solve the problem, we need to find the dimensions of x and the value of y in the equation:
P=nxyTV0e−MghnxT
where:
- n is the number of moles,
- P represents acceleration due to gravity,
- h is height,
- M is mass,
- g is acceleration due to gravity,
- T is temperature,
- V0 is volume.
Step 1: Analyze the Exponential Term
The term e−MghnxT must be dimensionless. This means that the dimensions of Mgh must equal the dimensions of nxT.
Step 2: Write Down the Dimensions
1. Dimensions of Mgh:
- M (mass) has dimensions (M).
- g (acceleration due to gravity) has dimensions (L)(T−2).
- h (height) has dimensions (L).
Therefore, the dimensions of Mgh are:
(Mgh)=(M)(L)(T−2)(L)=(M)(L2)(T−2)
2. Dimensions of nxT:
- n (number of moles) has dimensions (μ).
- x has unknown dimensions (x).
- T (temperature) has dimensions (K).
Therefore, the dimensions of nxT are:
(nxT)=(μ)(x)(K)
Step 3: Set the Dimensions Equal
Since Mgh and nxT must have the same dimensions:
(M)(L2)(T−2)=(μ)(x)(K)
Step 4: Solve for the Dimensions of x
Rearranging gives:
(x)=(M)(L2)(T−2)(μ)(K)
Thus, the dimensions of x are:
(x)=(M1L2T−2μ−1K−1)
Step 5: Determine the Value of y
Next, we need to find the value of y. From the equation, we know that P represents pressure, which has dimensions:
(P)=(M)(L−1)(T−2)
Now, we can express P in terms of n,x,T, and V0:
(P)=(μ)(xy)(K)(L3)
Rearranging gives:
(P)(L3)=(μ)(xy)(K)
Substituting the dimensions:
(M)(L−1)(T−2)(L3)=(μ)(xy)(K)
This simplifies to:
(M)(L2)(T−2)=(μ)(xy)(K)
Step 6: Substitute for x
Substituting (x) into the equation:
(M)(L2)(T−2)=(μ)((M)(L2)(T−2)(μ)(K))y(K)
Step 7: Solve for y
After simplification, we find that y=1 since the dimensions must balance out.
Conclusion
Thus, we have:
- The dimensions of x are (M1L2T−2μ−1K−1).
- The value of y is 1.
- n is the number of moles,
- P represents acceleration due to gravity,
- h is height,
- M is mass,
- g is acceleration due to gravity,
- T is temperature,
- V0 is volume.
- M (mass) has dimensions (M).
- g (acceleration due to gravity) has dimensions (L)(T−2).
- h (height) has dimensions (L).
(Mgh)=(M)(L)(T−2)(L)=(M)(L2)(T−2)
- n (number of moles) has dimensions (μ).
- x has unknown dimensions (x).
- T (temperature) has dimensions (K).
(nxT)=(μ)(x)(K)
(M)(L2)(T−2)=(μ)(x)(K)
(x)=(M)(L2)(T−2)(μ)(K)
(x)=(M1L2T−2μ−1K−1)
(P)=(M)(L−1)(T−2)
(P)=(μ)(xy)(K)(L3)
(P)(L3)=(μ)(xy)(K)
(M)(L−1)(T−2)(L3)=(μ)(xy)(K)
(M)(L2)(T−2)=(μ)(xy)(K)
(M)(L2)(T−2)=(μ)((M)(L2)(T−2)(μ)(K))y(K)
- The dimensions of x are (M1L2T−2μ−1K−1).
- The value of y is 1.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
8 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE
20 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION H (Multiple True-False)
6 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
Similar Questions
The velocity of a freely falling body changes as gphqwhere g is acceleration due to gravity and h is the height. The values of p and q are
View SolutionLet us consider an equaiton
12mv2=mgh,
Where m is the mass of the body, υ its velocity, g is acceleration due to gravity and h is the height. Cheak whether this equation is dimensionally correct.
View Solution
Knowledge Check
An object lauched upwards at an angle has parabolic motion. The height h, of a projectile at time t is given by the equation h=12at2+vyt+h0, where a is the acceleration due to gravity, vv is the vertical component of the velocity, and h0 is the initial height. Which of the following equations correctly represents the object's acceleration due to gravity in terms of the other variables ?
Aa=h−vvt−h0tBa=h−vvt−h02t2Ca=2(h−vvt−h0)t2Da=t√2(h−vvt−h0)
Acceleration due to gravity as same at height h from surface and at depth d from surface, then find value of d
View SolutionA freely body acquires a velocity of gxhy after falling through a height h. Using dimensions find the values fo x and y.
View SolutionThe Bernoulli's equation is given by P+12ρv2+hρg=k. Where P= pressure, ρ= density, v= speed, h=height of the liquid column, g= acceleration due to gravity and k is constant. The dimensional formula for k is same as that for:
View SolutionIn the equation (1pβ)=ykBT, where p is the pressure, y is the distance, kB is Boltzmann constant and T is the tempreture. Dimensions of β are
View SolutionIn the formula , p=nRTV−beaRTV find the dimensions of a and b, where p = pressure , n= number of moles , T = temperture , V = volume and R = universal gas constant .
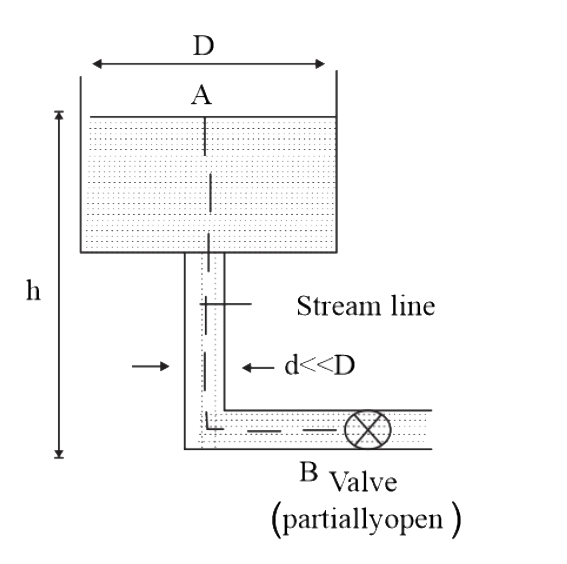
View SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
View SolutionA projectile is fired with speed v0 at t=0 on a planet named ' Increasing Gravity ' . This planet is strange one, in the sense that the acceleration due to gravity increases linearly with time t asg(t)=bt, where b is a positive constant. 'Increase Gravity'
If angle of projection with horizontal is θ, then the maximum height attained is
View Solution
