Consider a chessboard of size 8 units ×8 units (i.e., each small square on the board has a side length of 1 unit). Let S be the set of all the 81 vertices of all the squares on the board. What is number of line segments whose vertices are in S1 and whose length is a positive integer? (The segments need not be parallel to the sides of the board).
The correct Answer is:780
Topper's Solved these Questions
- COMBINATORICSBOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-I: Previous Asked Question for Pre RMO)
23 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - High Level Problems (HLP)
33 Videos
- DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCECHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - High Level Problem
37 Videos
Similar Questions
Let each side of smallest square of chess board in one unit in length. Find the sum of area of all possible squares whose side parallel to side of chess board.
View Solution15. Write the coordinates of the vertices of a square whose each side is 5units, one vertex at (2,1) and all the vertices lie in the same quadrant.
View Solution
Knowledge Check
In the grid shown below , each small square has a side length of 1 unit . In the shaded region , each vertex lies on a vertex of a small square . What is the area , in square units , of the shaded region ?
 A35B25C24D19
A35B25C24D19
Let each side of smallest square of chess boards is one unit in length. Find the total number of rectangles (including squares) whose side parallel to side of chess board
View SolutionConsider square ABCD of side length 1. Let P be the set of all segments of length 1 with endpoints on the adjacent sides of square ABCD . The midpoints of segments in P enclose a region with area A. The value of A is (a) π4 (b) 1−π4 (c) 4−π4 (d) none of these
View SolutionThe following figures are made of 5 squares each square has side of 1 unit length. Find the perimeter of each of the given
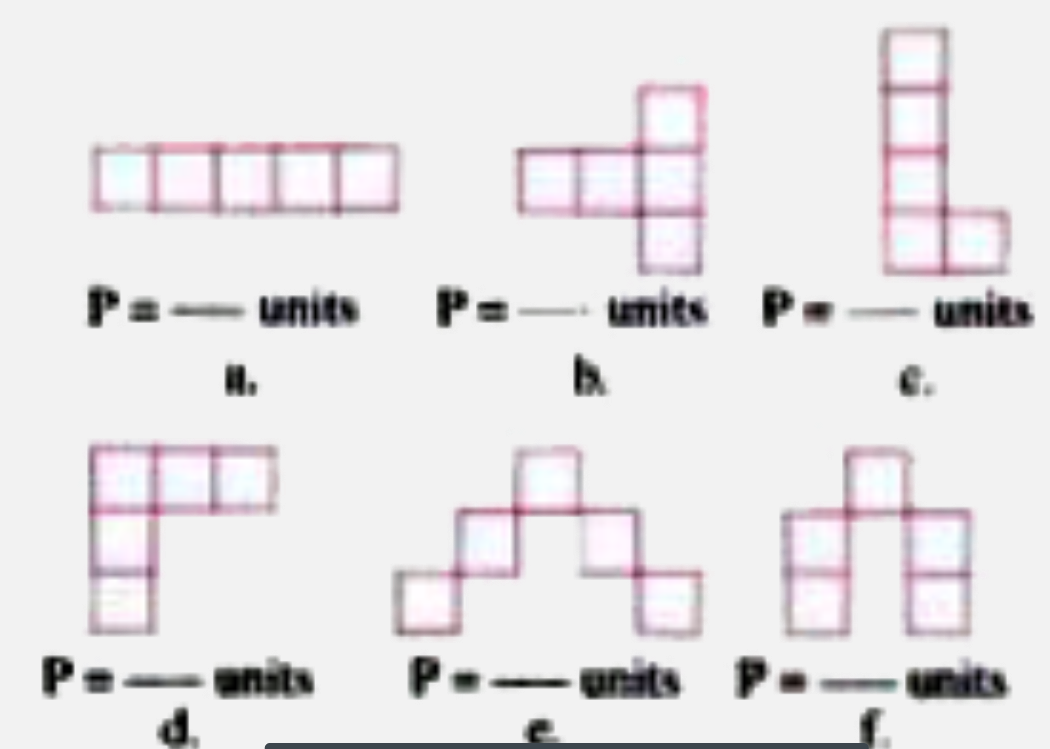
View SolutionNumber of ways in which 3 squares of unit length can be chosen on a 8 x 8 chessboard, so that all squares are in same diagonal line, is
View SolutionConsider square ABCD of side length 1. Let P be the set of all segments of length 1 with endpoints on the adjacent sides of square ABCD . The midpoints of segments in P enclose a region with area A. The value of A is (a) π4 (b) 1−π4 (c) 4−π4 (d) none of these
View SolutionA rectangular field is of length 10 units & breadth 8 units. One of its vertex lie on the origin. The longer side is along x-axis and one of its vertices lie in first quadrant. Find all the vertices.
View SolutionIn the Figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
View Solution
