A block of mass 50kg rests on a rough horizontal plane whose coefficient of static friction is 0.3. What is the least force required to just move it if it is pulled (i) horizontally and (ii) at 45∘ to the horizontal.
The correct Answer is:(i)147N (ii)103.96N
To solve the problem step by step, we need to determine the least force required to move a block of mass 50 kg resting on a rough horizontal plane with a coefficient of static friction of 0.3 in two scenarios: (i) when pulled horizontally and (ii) when pulled at an angle of 45 degrees to the horizontal.
Step 1: Calculate the Normal Force (N)
The normal force (N) acting on the block can be calculated using the formula:
N=mg
Where:
- m=50kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
Calculating:
N=50kg×10m/s2=500N
Step 2: Calculate the Maximum Static Friction Force (f)
The maximum static friction force can be calculated using the formula:
f=μsN
Where:
- μs=0.3 (coefficient of static friction)
Calculating:
f=0.3×500N=150N
Step 3: Case (i) - Force Required When Pulled Horizontally
When the block is pulled horizontally, the force required to overcome static friction is equal to the maximum static friction force calculated in Step 2.
Thus, the least force required to just move the block when pulled horizontally is:
F=150N
Step 4: Case (ii) - Force Required When Pulled at 45 Degrees
When the block is pulled at an angle of 45 degrees, we need to consider both the vertical and horizontal components of the applied force (F).
1. Vertical Component:
Fy=Fsin(45∘)=F√2
2. Horizontal Component:
Fx=Fcos(45∘)=F√2
Using the equilibrium of forces in the vertical direction:
N+Fy=mg
Substituting for Fy:
N+F√2=500
Rearranging gives:
N=500−F√2
Using the equilibrium of forces in the horizontal direction:
Fx=f
Substituting for Fx and f:
F√2=μsN
Substituting N:
F√2=0.3(500−F√2)
Step 5: Solve for F
Expanding and rearranging the equation:
F√2=150−0.3F√2
Combining like terms:
F√2+0.3F√2=150
1.3F√2=150
Multiplying both sides by √2:
1.3F=150√2
Dividing by 1.3:
F=150√21.3
Calculating F:
F≈150×1.4141.3≈163.15N
Final Answers
1. The least force required to just move the block when pulled horizontally is 150 N.
2. The least force required to just move the block when pulled at an angle of 45 degrees is approximately 163.15 N.
The normal force (N) acting on the block can be calculated using the formula:
N=mg
Where:
- m=50kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
N=50kg×10m/s2=500N
The maximum static friction force can be calculated using the formula:
f=μsN
Where:
- μs=0.3 (coefficient of static friction)
f=0.3×500N=150N
When the block is pulled horizontally, the force required to overcome static friction is equal to the maximum static friction force calculated in Step 2.
F=150N
When the block is pulled at an angle of 45 degrees, we need to consider both the vertical and horizontal components of the applied force (F).
Fy=Fsin(45∘)=F√2
Fx=Fcos(45∘)=F√2
N+Fy=mg
Substituting for Fy:
N+F√2=500
N=500−F√2
Fx=f
Substituting for Fx and f:
F√2=μsN
Substituting N:
F√2=0.3(500−F√2)
Expanding and rearranging the equation:
F√2=150−0.3F√2
Combining like terms:
F√2+0.3F√2=150
1.3F√2=150
Multiplying both sides by √2:
1.3F=150√2
Dividing by 1.3:
F=150√21.3
F≈150×1.4141.3≈163.15N
1. The least force required to just move the block when pulled horizontally is 150 N.
2. The least force required to just move the block when pulled at an angle of 45 degrees is approximately 163.15 N.
Topper's Solved these Questions
Similar Questions
A block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionA block of mass 5kg is placed on a rough horizontal plane whose coefficient of friction is 0.3. Find the least horizontal force needed to move the block along the plane and the resultant of normal reaction and the force applied.
View SolutionA weight W rests on a rough horizontal plane,If the angle of friction is θ,the least force that can move the body along the plane will be
View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and g=10ms−2 The frictional force on the block is
View SolutionA block of weight 100N is lying on a rough horizontal surface. If coefficient of friction 1/√3. The least possible force that can move the block is
View SolutionA block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View SolutionA block of mass 1kg is at rest on a rough horizontal surface having coefficient of static friction 0.2 and kinetic friciton 0.15, find the frictional forces if a horizontal force,
(a) F=1N (b) F=1.96N (c) F=2.5N is applied on a block

View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
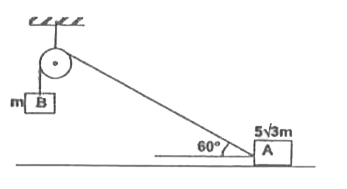
View SolutionA block A of mass 5√3m rests on a rough horizontal plane relative to which its coefficient of friction is μA light string attached to this block passes over a light frictionless pulley and another block B of mass m hangs from it. It is observed that the block A just slips when the string makes an angle of 60∘ with the horizontal .
Find the coefficient of static friction between the block A and the plane. If the same force acting through the sting is applied to the block A in the horizontal direction, find the acceleration of the block A.
View Solution
