Question

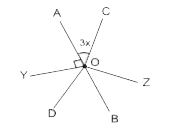
The line segments AB and CD intersect at O. OF is the internal bisector of obtuse angle BOC and OE is the internal bisector of acute angle AOC. If $\angle BOC={130}^{\circ }$, what is the measure of $\angle FOE$?

Options

A. `90^(@)`
B. `110^(@)`
C. `115^(@)`
D. `120^(@)`

Explanation

To solve the problem step by step, we can follow these instructions:

Step 1: Understand the given information
We have two line segments AB and CD intersecting at point O. The angle BOC is given as 130 degrees. OF is the internal bisector of the obtuse angle BOC, and OE is the internal bisector of the acute angle AOC.

Step 2: Identify the angles
Since angle BOC is 130 degrees, we can denote:
- Let angle BOC = 130 degrees
- Let angle AOC = x degrees (we will find this later)

Step 3: Find the angles created by the bisectors
Since OF is the internal bisector of angle BOC, it divides angle BOC into two equal parts:
- Let angle 1 = angle 2 = angle BOC / 2 = 130 degrees / 2 = 65 degrees.

Now we know:
- angle 1 = 65 degrees
- angle 2 = 65 degrees

Step 4: Determine angle AOC
Since the angles around point O must sum up to 360 degrees, we can find angle AOC:
- angle AOC = 360 degrees - angle BOC - angle AOB (where AOB is the angle opposite to AOC).
- Since angle BOC is 130 degrees, the remaining angles (AOB + AOC) must equal 230 degrees.

Step 5: Find the internal bisector of angle AOC
Let angle AOC = x degrees. The internal bisector OE will divide angle AOC into two equal parts:
- Let angle 3 = angle 4 = x / 2.

Step 6: Use the linear pair property
The angles around point O must add up to 360 degrees:
- angle 1 + angle 2 + angle 3 + angle 4 = 180 degrees (since we are only considering the angles around point O).
- Therefore, we can write:
65 + 65 + (x/2) + (x/2) = 180
- This simplifies to:
130 + x = 180
- Thus, x = 50 degrees.

Step 7: Calculate angle FOE
Now we know:
- angle AOC = 50 degrees
- angle 3 = angle 4 = 50 / 2 = 25 degrees.

Finally, angle FOE can be calculated as:
- angle FOE = angle 1 + angle 3 = 65 + 25 = 90 degrees.

Conclusion
Therefore, the measure of angle FOE is 90 degrees.