If AB is a chord of a circle, P and Q are two points on the circle different from A and B, then:
the angle subtended by AB at P and Q are either equal or supplementary
the sum of the angles subtended by AB at P and q is always equal two right angles
the angles subtended at P and Q by AB are always equal
the sum of the angles subtended at P and q is equal to four right angles
The correct Answer is:A
Step by step video, text & image solution for If AB is a chord of a circle, P and Q are two points on the circle different from A and B, then: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If AB is a chord of a circle, Pand Q are the two points on the circle different from A and B, then ∠APB= ∠AQB ∠APB+∠AQB=180∘ or∠APB= ∠AQB
View SolutionAB is a chord of a circle with O as centre. C is a point on the circle such that OC is perpendicular to AB and OC intersects AB at P. If PC = 2 cm and AB = 6 cm then the diameter of the circle is
View Solution
Knowledge Check
A point charge q is held at the centre of a circle of radius r. B,C are two points on the circumference of the circle and A is a point outsdie the circle . If WAB charge qe from A to B and WAC represents the workdone from A to C ,then
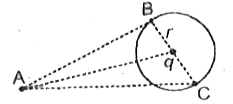 AWAB>WACBWAB<WACCWAB=WAC≠0DWAB=WAC=0
AWAB>WACBWAB<WACCWAB=WAC≠0DWAB=WAC=0AB is a chord to a circle and PAT is the tangent to the circle at A. If ∠BAT=75∘and∠BAC=45∘, C being a point on the circle, then ∠ABC is equal to
A40∘B45∘C60∘D70∘If a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
A30∘B60∘C90∘D120∘
AB is a diameter of a circle. P is a point on the semi-circle APB.AHandBK are perpendiculars from AandB respectively to the tangent at P. Prove that AH+BK=AB.
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View SolutionPA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If ∠APB=70∘ then ∠OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
View Solution
