In a quadrilateral ABCD, ∠B=∠C=60∘and∠D=90∘. Find the length of CD, if AD=3√3andBC=6√3cm.
1. 3(2√3−1)cm
2. 6(√3−1)cm
3. 2(3√3−1)cm
4. √3(2√3−1)cm
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the given information
We have a quadrilateral ABCD with the following angles:
- ∠B=60∘
- ∠C=60∘
- ∠D=90∘
We are also given the lengths:
- AD=3√3 cm
- BC=6√3 cm
Step 2: Draw the figure
Draw quadrilateral ABCD with the given angles and label the sides accordingly.
Step 3: Draw parallel lines
Draw a line parallel to AC from point A to point E, and another parallel line from point D to point F. This will help us in applying trigonometric ratios.
Step 4: Analyze triangle EFC
In triangle EFC, since EF is parallel to AD, we can use the sine ratio:
sin60∘=EFEC
Given that EF=AD=3√3, we can substitute:
√32=3√3EC
Step 5: Solve for EC
Cross-multiplying gives:
EC=3√3√32=6 cm
Step 6: Find BE
Now, we know BC=6√3 cm, so:
BE=BC−EC=6√3−6
Step 7: Find AE
Since ∠ABE=60∘ and ∠AEF=90∘, triangle ABE is also 60-60-60, making it an equilateral triangle. Thus:
AE=BE=6√3−6
Step 8: Find FD
Since FD is parallel to AE, we have:
FD=AE=6√3−6
Step 9: Analyze triangle EFC again
In triangle EFC, we can use the tangent ratio:
tan60∘=EFFC
Substituting the values:
√3=3√3FC
Step 10: Solve for FC
Cross-multiplying gives:
FC=3√3√3=3 cm
Step 11: Find CD
Finally, we can find CD:
CD=BE+FC=(6√3−6)+3
CD=6√3−3
Step 12: Factor out the common term
Factoring out the common term gives:
CD=3(2√3−1) cm
Final Answer
Thus, the length of CD is 3(2√3−1) cm.
---
We have a quadrilateral ABCD with the following angles:
- ∠B=60∘
- ∠C=60∘
- ∠D=90∘
- AD=3√3 cm
- BC=6√3 cm
Draw quadrilateral ABCD with the given angles and label the sides accordingly.
Draw a line parallel to AC from point A to point E, and another parallel line from point D to point F. This will help us in applying trigonometric ratios.
In triangle EFC, since EF is parallel to AD, we can use the sine ratio:
sin60∘=EFEC
Given that EF=AD=3√3, we can substitute:
√32=3√3EC
Cross-multiplying gives:
EC=3√3√32=6 cm
Now, we know BC=6√3 cm, so:
BE=BC−EC=6√3−6
Since ∠ABE=60∘ and ∠AEF=90∘, triangle ABE is also 60-60-60, making it an equilateral triangle. Thus:
AE=BE=6√3−6
Since FD is parallel to AE, we have:
FD=AE=6√3−6
In triangle EFC, we can use the tangent ratio:
tan60∘=EFFC
Substituting the values:
√3=3√3FC
Cross-multiplying gives:
FC=3√3√3=3 cm
Finally, we can find CD:
CD=BE+FC=(6√3−6)+3
CD=6√3−3
Factoring out the common term gives:
CD=3(2√3−1) cm
Thus, the length of CD is 3(2√3−1) cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a quadrilateral ABCD,∠A+∠C=180∘, then ∠B+∠D is equal to
A360∘B100∘C180∘D80∘ - Question 2 - Select One
In a quadrilateral ABCD, ∠A:∠B:∠C:∠D=3:4:5:6. Then ABCD is a __________
AtrapeziumBparallelogramCrhombusDkite
In a ΔABC,∠C=3∠B=2(∠A+∠B) find the three angles.
View SolutionIn the quadrilateral ABCD,AC=8√3cm, angle CAB=30∘ angle ADC=60∘ angle ABC = angle ACD=90∘. Find the area of the quadrilateral ABCD.
View SolutionIn quadrilateral ABCD, AB = AD and BC = CD. Show that ∠ABC=∠ADC.
 View Solution
View SolutionIn the given quadrilateral ABCD,AB=15cm,BC=20cmandAD=7cm∠ABC=∠ADC=90∘. Find the length of side CD:
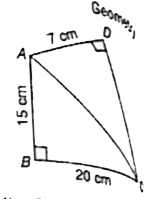 View Solution
View SolutionIn a quadrilateral ABCD,AB=5cm,BC=37cm,CD=35cm,BD=12cm and AD=13cm . Find its area
View SolutionABCD is a cyclic quadrilateral. If AD∣∣BCand∠B=70∘, find the other angles of ABCD.
View Solution

