Question

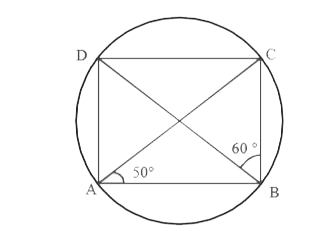
ABCD is a cyclic quadrilateral. If $AD\mid \mid BC\text{and}\angle B={70}^{\circ },$ find the other angles of ABCD.

Answer

`angle A = 110^(@), angla C = 70^(@), angle D = 110^(@)`

Explanation

To solve the problem, we need to find the angles of the cyclic quadrilateral ABCD given that AD is parallel to BC and angle B is 70 degrees.

1. Identify the Given Information:
- We know that ABCD is a cyclic quadrilateral.
- AD is parallel to BC.
- Angle B = 70 degrees.

2. Use the Property of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, the sum of opposite angles is equal to 180 degrees.
- Therefore, we can write the equation for angles B and D:
\( \text{Angle B} + \text{Angle D} = 180^\circ \)
- Substituting the value of angle B:
\( 70^\circ + \text{Angle D} = 180^\circ \)

3. Calculate Angle D:
- Rearranging the equation gives us:
\( \text{Angle D} = 180^\circ - 70^\circ = 110^\circ \)

4. Use the Parallel Lines Property:
- Since AD is parallel to BC, we can use the property of alternate interior angles.
- Therefore, we have:
\( \text{Angle D} = \text{Angle A} + \text{Angle B} \)
- This means:
\( 110^\circ = \text{Angle A} + 70^\circ \)

5. Calculate Angle A:
- Rearranging gives us:
\( \text{Angle A} = 110^\circ - 70^\circ = 40^\circ \)

6. Find Angle C Using Opposite Angles Property:
- Again, using the property of cyclic quadrilaterals:
\( \text{Angle A} + \text{Angle C} = 180^\circ \)
- Substituting the value of angle A:
\( 40^\circ + \text{Angle C} = 180^\circ \)

7. Calculate Angle C:
- Rearranging gives us:
\( \text{Angle C} = 180^\circ - 40^\circ = 140^\circ \)

Summary of Angles:
- Angle A = 110 degrees
- Angle B = 70 degrees
- Angle C = 140 degrees
- Angle D = 110 degrees

Final Answer:
- Angle A = 110°
- Angle B = 70°
- Angle C = 140°
- Angle D = 110°