250 students appeared in MOCK CAT consisting of three sections viz. Maths, Data Interpretation (DI) and English. 20 students did not qualify any of the three sections and 66 students qualified all the three sections, 24 students did not qualify DI only. 12 did not qualify DI and Maths only. Those who qualified Maths only exceeded those who did not qualify any of the section by 16. Those who did not qualify Maths only exceeded those who did not qualify only DI and Maths by 8. Those who did not qualify English only were twice the number of students who did not qualify Maths only. Find the number of students who has qualified atleast two sections.
To solve the problem step by step, we will define variables for each group of students based on their qualifications in the three sections: Maths (M), Data Interpretation (DI), and English (E).
1. Define Variables:
- Let x be the number of students who qualified only Maths.
- Let y be the number of students who qualified only DI.
- Let z be the number of students who qualified only English.
- Let a be the number of students who qualified both Maths and DI but not English.
- Let b be the number of students who qualified both Maths and English but not DI.
- Let c be the number of students who qualified both DI and English but not Maths.
- Let d be the number of students who qualified all three sections (given as 66).
- We know that 20 students did not qualify any section.
2. Total Students:
The total number of students is given as 250. Therefore, we can write the equation:
x+y+z+a+b+c+d+20=250
Substituting d=66:
x+y+z+a+b+c+66+20=250
Simplifying gives:
x+y+z+a+b+c=164(Equation 1)
3. Students Not Qualifying DI:
We know that 24 students did not qualify DI only, meaning they either did not qualify Maths or English or both. This can be expressed as:
20+z+x+12+a+b=24
Rearranging gives:
z+x+a+b=4(Equation 2)
4. Students Not Qualifying DI and Maths:
It is given that 12 students did not qualify DI and Maths only. This means:
c=12(Equation 3)
5. Students Qualifying Maths Only:
The number of students who qualified Maths only exceeds those who did not qualify any section by 16:
x=20+16=36(Equation 4)
6. Students Not Qualifying Maths Only:
The number of students who did not qualify Maths only exceeds those who did not qualify only DI and Maths by 8. The number of students who did not qualify only DI and Maths is 12:
y+c+z+20=12+8
Therefore:
y+z+20=20⇒y+z=0(Equation 5)
7. Students Not Qualifying English Only:
Those who did not qualify English only were twice the number of students who did not qualify Maths only. The number of students who did not qualify Maths only is:
20+z+y+12+a+b=20+0+12+a+b=32
Therefore:
2×32=64⇒c=64(Equation 6)
8. Substituting Values:
Now we can substitute the known values into the equations:
- From Equation 4: x=36
- From Equation 3: c=12
- From Equation 5: y=0 and z=0
Substitute these into Equation 1:
36+0+0+a+b+12+66+20=250
Simplifying gives:
a+b=164−36−12−66−20=34
9. Finding Students Qualifying at Least Two Sections:
Students qualifying at least two sections are those who qualified:
- Both Maths and DI (a)
- Both Maths and English (b)
- Both DI and English (c)
- All three sections (d)
Therefore:
At least two sections=a+b+c+d=a+b+12+66
Since a+b=34:
=34+12+66=112
Thus, the number of students who qualified at least two sections is 112.
- Let x be the number of students who qualified only Maths.
- Let y be the number of students who qualified only DI.
- Let z be the number of students who qualified only English.
- Let a be the number of students who qualified both Maths and DI but not English.
- Let b be the number of students who qualified both Maths and English but not DI.
- Let c be the number of students who qualified both DI and English but not Maths.
- Let d be the number of students who qualified all three sections (given as 66).
- We know that 20 students did not qualify any section.
The total number of students is given as 250. Therefore, we can write the equation:
x+y+z+a+b+c+d+20=250
Substituting d=66:
x+y+z+a+b+c+66+20=250
Simplifying gives:
x+y+z+a+b+c=164(Equation 1)
We know that 24 students did not qualify DI only, meaning they either did not qualify Maths or English or both. This can be expressed as:
20+z+x+12+a+b=24
Rearranging gives:
z+x+a+b=4(Equation 2)
It is given that 12 students did not qualify DI and Maths only. This means:
c=12(Equation 3)
The number of students who qualified Maths only exceeds those who did not qualify any section by 16:
x=20+16=36(Equation 4)
The number of students who did not qualify Maths only exceeds those who did not qualify only DI and Maths by 8. The number of students who did not qualify only DI and Maths is 12:
y+c+z+20=12+8
Therefore:
y+z+20=20⇒y+z=0(Equation 5)
Those who did not qualify English only were twice the number of students who did not qualify Maths only. The number of students who did not qualify Maths only is:
20+z+y+12+a+b=20+0+12+a+b=32
Therefore:
2×32=64⇒c=64(Equation 6)
Now we can substitute the known values into the equations:
- From Equation 4: x=36
- From Equation 3: c=12
- From Equation 5: y=0 and z=0
36+0+0+a+b+12+66+20=250
Simplifying gives:
a+b=164−36−12−66−20=34
Students qualifying at least two sections are those who qualified:
- Both Maths and DI (a)
- Both Maths and English (b)
- Both DI and English (c)
- All three sections (d)
At least two sections=a+b+c+d=a+b+12+66
Since a+b=34:
=34+12+66=112
Topper's Solved these Questions
Similar Questions
Find the 11th term of -2,3,8,13………
View SolutionWhich of the following is/are the solution(s) of x2−7×+12=0
View SolutionTwo students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that (a) Both Anil and Ashima will not qualify the examination. (b) Atleast one of them will not qualify the examination and (c) Only one of them will qualify the examination.
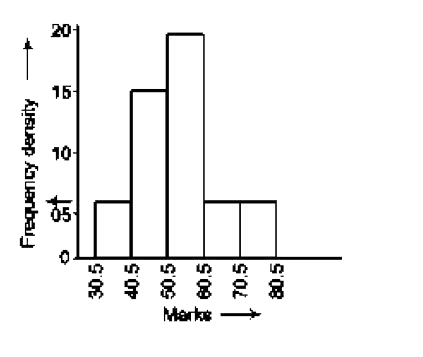
View SolutionA student is marked as 'qualified', if he obtain marks above 40.5. Here, the ratio of the number of qualified student to those who are not qualified, is
View Solution250 students appeared in MOCK CAT consisting of three sections viz. Maths, Data Interpretation (DI) and English. 20 students did not qualify any of the three sections and 66 students qualified all the three sections, 24 students did not qualify DI only. 12 did not qualify DI and Maths only. Those who qualified Maths only exceeded those who did not qualify any of the section by 16. Those who did not qualify Maths only exceeded those who did not qualify only DI and Maths by 8. Those who did not qualify English only were twice the number of students who did not qualify Maths only. Find the number of students who has qualified atleast two sections.
View SolutionIn a 12 -storey house ten people enter a lift cabin. It is known that they will left in groups of 2,3 and 5 people at different storeys. The number of ways they can do so if the left does not stop to the second storey is
View SolutionA person writes letters to six friends and be the number of ways so that at least two of the number of ways so that all the letters are in wrong envelopes. Then x−y=
View SolutionA person invites a party of 10 friends at dinner and place them so that 4 are on one round table and 6 on the other round table. The number of ways in which he can arrange the guests is
View SolutionThe different letters of the alphabet are given, Out of which five letter words are formed. Then the numbers of words in which at least one letter is repeated is
View SolutionThere are 18 points in a plane such that no three of them are in the same line except five points which are collinear. The number of triangles formed by these points is:
View SolutionTwo students Anil and Ashima appeared is an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability qualify the examination is 0.02. Find the probability that
(a) Bothe Anil and Ashima will not qualify the examination.
(b) Atleast one of them will qualify the examination and (c) Only one of them will qualify the examination.
View SolutionTwo students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that(a) Both Anil and Ashima will not qualify the examination.(b) Atleast one of them will not qualify the examination and(c) Only one of them will qualify the examination.
View SolutionTwo students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that (a) Both Anil and Ashima will not qualify the examination. (b) Atleast one of them will not qualify the examination and (c) Only one of them will qualify the examination.
View SolutionTwo students Anil and ashima appeared in an examination.The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10.The probability that both will qualify the examination is 0.02.Find the probability that (c)Only one of them will qualify the examination.
View SolutionNumber of aspirants who had qualified only in DI section
View Solution
