A quadratic equation has double root, then

A

the two roots lie on the different sides of the axis

B

the quadratic equation cannot be expressed in the form of a perfect square.

C

the product of the roots is always negative.

D

the sum of the roots may be positive or negative.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for A quadratic equation has double root, then by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023
Class 14MATHSTHEORY OF EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Which one(s) of the following graphs is/are correctly sketched for the given quadratic equation which has double root (i.e., both the roots are equal), considering that all of these graphs appear considerably thick when seen, with a magnifying lens? The horizontal lines, in these graphs, represent the X-axis.
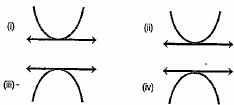    ocr_image

    A(A) (i) and (ii)
    B(B) (ii) and (iv)
    C(C) (i) and (iii)
    D(D) (ii) and (iii)

  • p : Every quadratic equation has one real root and q Every quadratic equation has two real roots, then truth value of p and q are:

    Ap is true and q is false
    Bp is false and q is true
    Cp and q both true
    Dp and g both false

  • If a quadratic equation has one real root then the other root will necessarily be

    Areal
    Bequal
    Ccomplex conjugate
    Drational and unequal