If the comprehensive graph of quadratic function lies in all the.four quadrants, then roots are necessarily
real
non-real
real and equal
equal and irrational
The correct Answer is:A
To solve the problem, we need to analyze the conditions under which a quadratic function can have its graph lie in all four quadrants of the Cartesian plane.
1. Understanding the Quadratic Function:
A quadratic function is generally expressed in the form f(x)=ax2+bx+c, where a, b, and c are constants. The graph of this function is a parabola.
Hint: Remember that the shape of the parabola depends on the coefficient a. If a>0, the parabola opens upwards; if a<0, it opens downwards.
2. Graph Behavior:
For the graph of the quadratic function to lie in all four quadrants, it must extend infinitely in both the positive and negative directions on the y-axis. This means that the parabola must cross the x-axis at two points (real roots).
Hint: Think about how the parabola must behave at extreme values of x to ensure it reaches both positive and negative y-values.
3. Roots of the Quadratic Function:
The roots of the quadratic function can be determined using the discriminant D=b2−4ac.
- If D>0, the quadratic has two distinct real roots.
- If D=0, the quadratic has one real root (a repeated root).
- If D<0, the quadratic has no real roots (the roots are complex or non-real).
Hint: Consider how the discriminant affects the number and type of roots.
4. Conclusion:
Since the graph of the quadratic function must cross the x-axis to lie in all four quadrants, it must have two distinct real roots. Therefore, the roots of the quadratic function are necessarily real.
Final Answer: The roots are necessarily real.
A quadratic function is generally expressed in the form f(x)=ax2+bx+c, where a, b, and c are constants. The graph of this function is a parabola.
For the graph of the quadratic function to lie in all four quadrants, it must extend infinitely in both the positive and negative directions on the y-axis. This means that the parabola must cross the x-axis at two points (real roots).
The roots of the quadratic function can be determined using the discriminant D=b2−4ac.
- If D>0, the quadratic has two distinct real roots.
- If D=0, the quadratic has one real root (a repeated root).
- If D<0, the quadratic has no real roots (the roots are complex or non-real).
Since the graph of the quadratic function must cross the x-axis to lie in all four quadrants, it must have two distinct real roots. Therefore, the roots of the quadratic function are necessarily real.
Topper's Solved these Questions
Similar Questions
Nature OF roots || Relation between roots & Coefficient || Graph OF quadratic equation || Formation OF quadratic equation when roots are given
View SolutionA quadratic equation is chosen from the set of all quadratic equations which are unchanged by squaring the roots. The chance that the chosen equation has equal root, is
View Solution
Knowledge Check
If a quadratic equation has one real root then the other root will necessarily be
ArealBequalCcomplex conjugateDrational and unequalConsider the following graph of a quadratic function. Then whichjof the following facts are true regarding this quadratic graph?
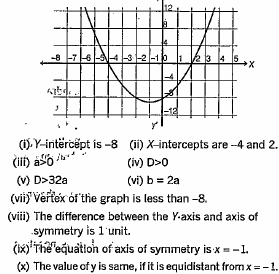 A(i),(ii), (iii) and (vi)B(ii),(iii),(iv) and (x)CExcept (v),(vi) and (x)Dall of these
A(i),(ii), (iii) and (vi)B(ii),(iii),(iv) and (x)CExcept (v),(vi) and (x)Dall of theseIf the roots of a quadratic equation are real and unequal, which one of the following is necessarily true?
AD<0BD = 0CD>0DD≥0
find variation in the values of all trignometric functions in different quadrants?
View SolutionArea enclosed by the graph of the function y=In2x−1 lying in the 4th quadrant is
View SolutionA quadratic equation is chosen from the set of all the quadratic equations which are unchaged by squaring their roots. The chance that the equation has unequal roots is
View SolutionLet →v1,→v2,→v3,→v4 be unit vectors in the xy-plane, one each in the interior of the four quadrants. Which of the following statements is necessarily ture. ?
View SolutionIf the minimum value of the quadratic function is 0, then which of the following is not definitely true, about the roots?
View Solution
