The graph of a quadratic equation is symmetrical about X-axis, which ones of the following can't be the roots of a quadratic equation?
A)(0,0)
B)(−23,23)
C)(2√3,−2√3)
D)(4+√2,4−√2)
The correct Answer is:D
To solve the problem, we need to analyze the properties of the roots of a quadratic equation whose graph is symmetrical about the X-axis. Let's break it down step by step.
Step 1: Understanding Symmetry about the X-axis
A quadratic equation can be expressed in the form ax2+bx+c=0. The graph of this equation is symmetrical about the X-axis if the roots of the equation are equal in magnitude but opposite in sign. This means if one root is α, the other root must be −α.
Step 2: Relationship Between Roots
If the roots are α and −α, we can express the sum of the roots as:
α+(−α)=0
This indicates that for the quadratic equation to be symmetrical about the X-axis, the sum of the roots must equal zero.
Step 3: Analyzing the Options
Now, we will evaluate the provided options to see which one does not satisfy the condition that the sum of the roots equals zero.
1. Option A: Roots are r1 and r2 such that r1+r2=0 (valid).
2. Option B: Roots are s1 and s2 such that s1+s2=0 (valid).
3. Option C: Roots are t1 and t2 such that t1+t2=0 (valid).
4. Option D: Roots are u1 and u2 such that u1+u2=8 (not valid).
Step 4: Conclusion
Since the requirement for the roots to be symmetrical about the X-axis is that their sum must be zero, we find that the fourth option, where the sum of the roots is 8, does not satisfy this condition. Therefore, this option cannot represent the roots of a quadratic equation that is symmetrical about the X-axis.
Final Answer
The option that cannot be the roots of a quadratic equation is Option D.
---
A quadratic equation can be expressed in the form ax2+bx+c=0. The graph of this equation is symmetrical about the X-axis if the roots of the equation are equal in magnitude but opposite in sign. This means if one root is α, the other root must be −α.
If the roots are α and −α, we can express the sum of the roots as:
α+(−α)=0
This indicates that for the quadratic equation to be symmetrical about the X-axis, the sum of the roots must equal zero.
Now, we will evaluate the provided options to see which one does not satisfy the condition that the sum of the roots equals zero.
2. Option B: Roots are s1 and s2 such that s1+s2=0 (valid).
3. Option C: Roots are t1 and t2 such that t1+t2=0 (valid).
4. Option D: Roots are u1 and u2 such that u1+u2=8 (not valid).
Since the requirement for the roots to be symmetrical about the X-axis is that their sum must be zero, we find that the fourth option, where the sum of the roots is 8, does not satisfy this condition. Therefore, this option cannot represent the roots of a quadratic equation that is symmetrical about the X-axis.
The option that cannot be the roots of a quadratic equation is Option D.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following ig not a graph of a quadratic equation?
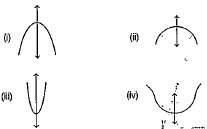 Aonly (iii)B(i) and (iii)C(ii) and (iv)Donly (iv)
Aonly (iii)B(i) and (iii)C(ii) and (iv)Donly (iv) - Question 2 - Select One
If the roots of a quadratic equation are unequal, which one of the following cannot be true?
AA)D>0BB)D<0CC)D = 0DD)Roots are conjugate also - Question 3 - Select One
Out of the following equations which one is nota quadratic equation ?
Ax2+4x=11+x2Bx2=4xC5x2=90D2x2−x2=x2+5
Which of the following is one root of the quadratic equation x2−7x+10=0
View SolutionWhich one is the quadratic equation?
View SolutionIf the two roots of a quadratic equation are −32 and −53 which one of the following is the concerned quadratic equation?
View SolutionIf the roots of a quadratic equation are real and unequal, which one of the following is necessarily true?
View SolutionIf 3/2 and 4 are the two roots of a quadratic equation, then which one of the following is the correct quadratic equation?
View Solution

