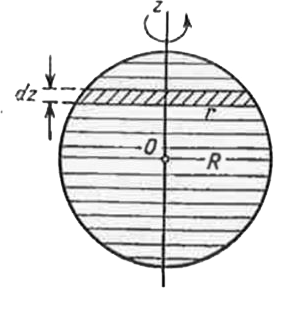
Derive, making use of an integral, the formula for the moment of inertia of a sphere about its diameter.

Text Solution

Verified by Experts

The correct Answer is: $0.4 M R^{2}$

Divide the sphere into thin disks perpendicular to the axis of rotation (Fig.) The differential of mass is
$d m = \frac{M π r^{2} d z}{4 / 3 π R^{3}} = \frac{3 M}{4 R^{3}} (R^{3} - z^{2}) d z$
Since $r^{2} = R^{2} - z^{2}$ . The moment of inertia of such a disk is
$d I = \frac{r^{2} d m}{2} = \frac{3 M}{8 R^{2}} (R^{2} - z^{2}) d z$
The moment of inertia of the sphere is
$I = 2 \int_{0}^{R} \frac{3 M}{8 R^{3}} (R^{4} - 2 R^{2} z^{2} + z^{4}) d z$ =
$= \frac{3 M}{4 R^{3}} [R^{4} \int_{0}^{R} d z - 2 R^{2} \int_{0}^{R} z^{2} d z + \int_{0}^{R} z^{4} d z] =$
$= \frac{3 M}{4 R^{3}} {[R^{4} z - 2 R^{2} \frac{z^{3}}{2} + \frac{z^{5}}{5}]}_{0}^{4} =$
$= \frac{3 M}{4 R^{3}} (R^{5} - \frac{2 R^{5}}{3} + \frac{R^{5}}{5}) = \frac{2}{5} M R^{2}$

Updated on:21/07/2023

|

Class 12 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

If temperature increases, the moment of inertia of a solid sphere about its diameter
Aincreases
Bdecreases
Cremains unchanged
Dbecomes negative
Two spheres of same mass and radius are in contact with each other. If the moment of inertia of a sphere about its diameter is I, then the moment of inertia of both the spheres about the tangent at their common point would be
A3I
B7I
C4I
D5I
With the increase in temperate, moment of inertia of a solid sphere about the diameter.
Adecreases
Bincreases
Cdoes not change
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile