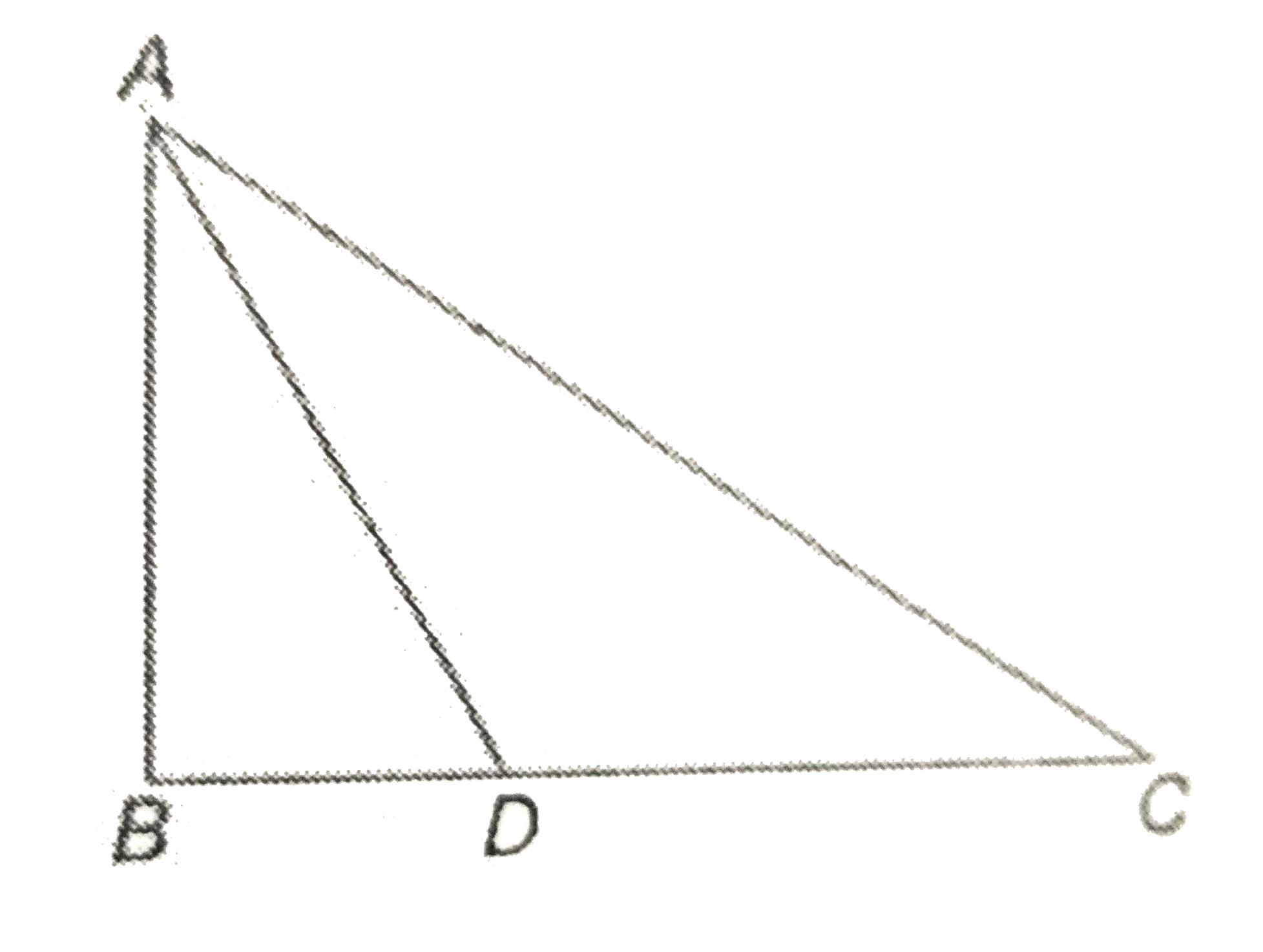
In the right angle ABC. BD divides the triangle ABC into two triangles of equal perimeters . Find the length of BD, given that AC=100,BC=80.∠B=90∘
The correct Answer is:24√5
To solve the problem, we need to find the length of segment BD in triangle ABC, where angle B is a right angle, AC = 100 cm, and BC = 80 cm. We know that BD divides triangle ABC into two triangles with equal perimeters.
1. Identify the Triangle Dimensions:
- We have triangle ABC with:
- AC = 100 cm (hypotenuse)
- BC = 80 cm (one leg)
- AB = ? (the other leg)
2. Calculate AB using Pythagorean Theorem:
- Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
AC2=AB2+BC2
1002=AB2+802
10000=AB2+6400
AB2=10000−6400=3600
AB=√3600=60 cm
3. Calculate the Perimeter of Triangle ABC:
- The perimeter (P) of triangle ABC is:
P=AB+BC+AC=60+80+100=240 cm
4. Set Up the Perimeter Equations for Triangles ABD and BDC:
- Let D be a point on AC. Denote:
- AD = x
- DC = 100 - x
- BD = y
- The perimeters of triangles ABD and BDC are:
- Perimeter of triangle ABD = AB + AD + BD = 60 + x + y
- Perimeter of triangle BDC = BC + DC + BD = 80 + (100 - x) + y = 180 - x + y
5. Set the Perimeters Equal:
- Since the perimeters are equal:
60+x+y=180−x+y
- Simplifying this gives:
60+x=180−x
2x=120
x=60
6. Substitute x back to find y:
- Now substitute x back into the perimeter equation:
60+60+y=180−60+y
- This simplifies to:
120+y=120+y
- This means y can be any value, but we need to find the length of BD.
7. Using the Right Triangle Properties:
- Since D divides AC into two equal segments (AD = DC), we can find BD using the right triangle properties:
- In triangle ABD:
BD2=AB2−AD2
BD2=602−602=0
- This means BD is equal to 0, which is not possible. We need to find the length of BD in terms of x and y.
8. Final Calculation:
- Since we have established that AD = 60 cm and DC = 40 cm, we can use the triangle properties to find BD.
- Using the right triangle properties again:
BD=√AB2−AD2
BD=√602−602=√0=0
Thus, the length of BD is 0 cm, which indicates that point D coincides with point A.
- We have triangle ABC with:
- AC = 100 cm (hypotenuse)
- BC = 80 cm (one leg)
- AB = ? (the other leg)
- Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
AC2=AB2+BC2
1002=AB2+802
10000=AB2+6400
AB2=10000−6400=3600
AB=√3600=60 cm
- The perimeter (P) of triangle ABC is:
P=AB+BC+AC=60+80+100=240 cm
- Let D be a point on AC. Denote:
- AD = x
- DC = 100 - x
- BD = y
- The perimeters of triangles ABD and BDC are:
- Perimeter of triangle ABD = AB + AD + BD = 60 + x + y
- Perimeter of triangle BDC = BC + DC + BD = 80 + (100 - x) + y = 180 - x + y
- Since the perimeters are equal:
60+x+y=180−x+y
- Simplifying this gives:
60+x=180−x
2x=120
x=60
- Now substitute x back into the perimeter equation:
60+60+y=180−60+y
- This simplifies to:
120+y=120+y
- This means y can be any value, but we need to find the length of BD.
- Since D divides AC into two equal segments (AD = DC), we can find BD using the right triangle properties:
- In triangle ABD:
BD2=AB2−AD2
BD2=602−602=0
- This means BD is equal to 0, which is not possible. We need to find the length of BD in terms of x and y.
- Since we have established that AD = 60 cm and DC = 40 cm, we can use the triangle properties to find BD.
- Using the right triangle properties again:
BD=√AB2−AD2
BD=√602−602=√0=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
ΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
A17B7C13D14D is a point on AC of the triangle with vertices A(2, 3), B(1, -3), C(-4, -7) and BD divides ABC into two triangles of equal area. The equation of the line drawn through B at right angles to BD is
Ay - 2x + 5 = 0B2y - x + 5 = 0Cy + 2x - 5 = 0D2y + x - 5 = 0In ΔABC,∠B is a right angle, AC=6 cm, D is the mid point of AC. The length of BD is
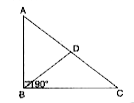 A4 cmB√6 cmC3 cmD3.5 cm
A4 cmB√6 cmC3 cmD3.5 cm
In a right angled triangle ABC, median BD divides right angle in 2 : 1 find the area of Δif BD = 10 cm ∠B=90∘
View SolutionIn triangle ABC, AB = 6, AC = 7 and BC = 8. If AD is bisector of angleA , then find the length of BD and CD.
View SolutionIn triangle ABC, if AD⊥BC and AD2=BD⋅DC. Then find the angle BAC
View SolutionIn a ΔABC (right angled at B) , median BD of length l divides angle B in the ratio of 2:1 . Find area of ΔABC .
View SolutionIn the triangle ABC,∠ABCor∠B=90∘.AB:BD:DC=3:1:3. If AC=20cm , then what is the length of AD (in cm) ?
View Solution