In right angle ΔABC, BD divides ΔABC into two equal perimeter Δ. Find AD if AC = 10 cm , BC = 8 cm ∠B=90∘
The correct Answer is:x=12√5
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the Triangle
We are given a right triangle ΔABC where:
- AC=10cm
- BC=8cm
- ∠B=90∘
Step 2: Find the Length of Side AB
Using the Pythagorean theorem:
AB2+BC2=AC2
Substituting the known values:
AB2+82=102
AB2+64=100
AB2=100−64=36
Taking the square root:
AB=√36=6cm
Step 3: Set Up the Perimeter Equation
Let AD=x and DB=y. Since BD divides ΔABC into two triangles with equal perimeters, we can write the perimeter of both triangles:
- Perimeter of ΔABD=AB+AD+BD=6+x+y
- Perimeter of ΔCBD=BC+CD+BD=8+(10−x)+y
Step 4: Set the Perimeters Equal
Set the two perimeters equal:
6+x+y=8+(10−x)+y
Simplifying this equation:
6+x+y=18−x+y
Subtracting y from both sides:
6+x=18−x
Adding x to both sides:
6+2x=18
Subtracting 6 from both sides:
2x=12
Dividing by 2:
x=6cm
Step 5: Conclusion
Since AD=x, we find that:
AD=6cm
Thus, the final answer is:
AD=6cm
---
We are given a right triangle ΔABC where:
- AC=10cm
- BC=8cm
- ∠B=90∘
Using the Pythagorean theorem:
AB2+BC2=AC2
Substituting the known values:
AB2+82=102
AB2+64=100
AB2=100−64=36
Taking the square root:
AB=√36=6cm
Let AD=x and DB=y. Since BD divides ΔABC into two triangles with equal perimeters, we can write the perimeter of both triangles:
- Perimeter of ΔABD=AB+AD+BD=6+x+y
- Perimeter of ΔCBD=BC+CD+BD=8+(10−x)+y
Set the two perimeters equal:
6+x+y=8+(10−x)+y
Simplifying this equation:
6+x+y=18−x+y
Subtracting y from both sides:
6+x=18−x
Adding x to both sides:
6+2x=18
Subtracting 6 from both sides:
2x=12
Dividing by 2:
x=6cm
Since AD=x, we find that:
AD=6cm
AD=6cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
The altitude AD of a ABC, in which ∠A obtuse and, AD=10cm. If BD=10cmandCD=10√3cm, determine ∠A.
A60∘B30∘C105∘DNone of theseWhat is the length of side AC in ΔABC which is right angled at B if BC = 5 cm and ∠BAC=30∘ ?
A5cmB15cmC10cmD7cmIn ΔABC, side BC = 10 cm and height AD = 4.4 cm If AC = 11 cm. then altitude BE equals -----
A5 cmB4 cmC5.6 cmD5.5 cm

In right -angled △ABC,BD⊥AC.
If AD =4 DC =9 then find BD.
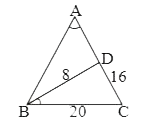
View SolutionIn this ΔABC,BD=8cm,BC=20cm,CD=16cmand∠CBD=∠CAB. Find the perimeter of ΔBDA.
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionIf ΔABC ~ ΔPQR, then evaluate the length of AC, if perimeter of ΔABC = 20 cm, perimeter of ΔPQR = 40 cm and PR= 8 cm.
View SolutionIn a right triangle ABC,∠B=90 . If AB=14 cm,BC=48 cm, find AC.
View Solution