In a ΔABC, angle bisector of interior angle A meets BC at D . if AB = 25 cm & AC = 20 cm If length of CD = 16 cm find length of BC ?
The correct Answer is:=12(B−C)
To solve the problem, we will use the Angle Bisector Theorem, which states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the lengths of the other two sides of the triangle.
1. Identify the Given Values:
- Length of AB = 25 cm
- Length of AC = 20 cm
- Length of CD = 16 cm
- Let BD = x cm (we need to find this)
2. Apply the Angle Bisector Theorem:
According to the Angle Bisector Theorem:
ABAC=BDCD
Substituting the known values:
2520=x16
3. Cross-Multiply to Solve for x:
Cross-multiplying gives us:
25⋅16=20⋅x
Simplifying this:
400=20x
4. Solve for x:
Divide both sides by 20:
x=40020=20 cm
Thus, BD = 20 cm.
5. Find the Length of BC:
Now, we can find the length of BC:
BC=BD+CD=20 cm+16 cm=36 cm
Final Answer:
The length of BC is 36 cm.
- Length of AB = 25 cm
- Length of AC = 20 cm
- Length of CD = 16 cm
- Let BD = x cm (we need to find this)
According to the Angle Bisector Theorem:
ABAC=BDCD
Substituting the known values:
2520=x16
Cross-multiplying gives us:
25⋅16=20⋅x
Simplifying this:
400=20x
Divide both sides by 20:
x=40020=20 cm
Thus, BD = 20 cm.
Now, we can find the length of BC:
BC=BD+CD=20 cm+16 cm=36 cm
The length of BC is 36 cm.
Topper's Solved these Questions
Similar Questions
The bisector of ∠A in △ABC meets BC in D. If AB = 15 cm, AC = 13 cm and BC = 14 cm, then DC =?
View SolutionIn △ABC, ∠A=90∘, AD is the bisector of ∠A meeting BC at D and DE⊥AC at E. If AB =10cm and AC = 15 cm, then the length of DE, in cm is:
△ABCमें ∠A=90∘, AD, ∠A का द्विभाजक है, जो BC से D पर मिलता है, और DE⊥AC से E पर मिलता है। यदि AB = 10 cm और AC= 15 cm है, तो DE की लंबाई(cm) है,View Solution
Knowledge Check
- Question 1 - Select One
In a △ABC,AD is the angle bisector of ∠CAB and a median to BC. If AC=15 cm, find AB.
AA)12 cmBB)18 cmCC)15 cmDD)can't be determined - Question 2 - Select One
In ΔABC, AD is the internal bisector of ∠A, meeting the side BC at D. If BD=5cm,BC=7.5cm, then AB:ACis
A2:1B1:2C4:5D3:5 - Question 3 - Select One
In △ABC, AD is the internal bisector of ∠S, meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then AB:AC is:
A3:5B4:5C1:2D2:1
In △ABC,the bisector of ∠A intersect side BC at D. If AB=12cm, AC =15cm and BC=18cm , then the length of BD is:
△ABC में, ∠A का द्विभाजक BC को D पर प्रतिच्छेदित करता है| यदि AB = 12cm, AC = 15cm और BC= 18cm है, तो BD की लंबाई है:View SolutionIn a triangle ABC, angle bisector of ∠BAC cut the side BD and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
View SolutionThe bisector of ∠B in △ABC meets AC at D. If AB = 10 cm, BC= 11 cm and AC = 14 cm, then the length of AD is:
△ABC में ∠B का समद्विभाजक AC से D पर मिलता है | यदि AB =10 सेमी, BC = 11 सेमी और AC =14 सेमी है, तो AD की लंबाई क्या होगी ?View SolutionIn the figure AD is the external bisector of ∠EAC, intersects BC produced to D. IF AB=12cm,AC=8cmandBC=4cm, find CD :
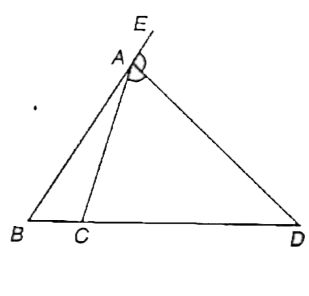 View Solution
View SolutionIn the triangle ABC, the internal bisector of angle A meets the side BC at D. If BD=7.5 cm and BC=9 cm. Then calculate the value of AB:AC.
View Solution

