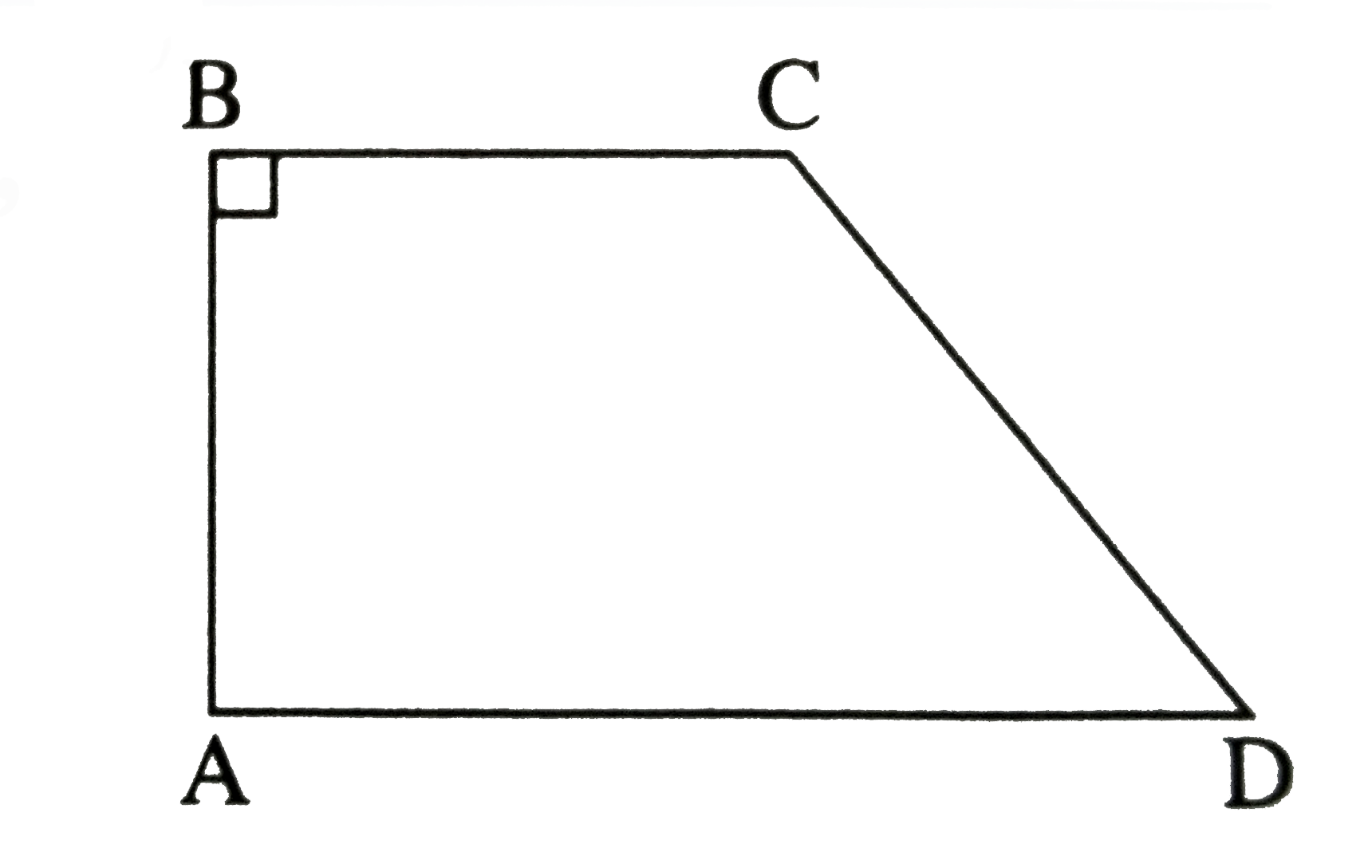
ABCDE is a pentagon. Ratio of sides AB : BC : CD : DE : EA is√2:1:2:1:√2. If ∠A=90∘ find its area if longer side is 6
The correct Answer is:27cm2
To find the area of pentagon ABCDE with the given side ratios and angle, we can follow these steps:
Step 1: Understand the Ratios
The sides of the pentagon are given in the ratio:
- AB : BC : CD : DE : EA = √2 : 1 : 2 : 1 : √2
Let’s denote the common unit for the ratios as x. Therefore, we can express the lengths of the sides as:
- AB = √2x
- BC = 1x
- CD = 2x
- DE = 1x
- EA = √2x
Step 2: Identify the Longer Side
We are given that the longer side of the pentagon is 6 cm. The longest side in the ratio is CD, which is 2x. Therefore, we have:
2x=6
From this, we can solve for x:
x=62=3
Step 3: Calculate the Lengths of Each Side
Now that we have x, we can find the lengths of all the sides:
- AB = √2×3=3√2 cm
- BC = 1×3=3 cm
- CD = 2×3=6 cm
- DE = 1×3=3 cm
- EA = √2×3=3√2 cm
Step 4: Calculate the Area of Triangle ABE
Since angle A is 90 degrees, triangle ABE is a right triangle. The area of triangle ABE can be calculated using the formula:
Area=12×base×height
Here, both the base (AB) and height (EA) are equal to 3√2:
AreaABE=12×3√2×3√2=12×9×2=9 cm2
Step 5: Calculate the Area of Rectangle BCDE
Next, we can find the area of rectangle BCDE. The length is CD = 6 cm and the breadth is BC = 3 cm:
AreaBCDE=length×breadth=6×3=18 cm2
Step 6: Calculate the Total Area of Pentagon ABCDE
Finally, we can find the total area of the pentagon by adding the areas of triangle ABE and rectangle BCDE:
Total Area=AreaABE+AreaBCDE=9+18=27 cm2
Final Answer
The area of pentagon ABCDE is 27 cm2.
---
The sides of the pentagon are given in the ratio:
- AB : BC : CD : DE : EA = √2 : 1 : 2 : 1 : √2
- AB = √2x
- BC = 1x
- CD = 2x
- DE = 1x
- EA = √2x
We are given that the longer side of the pentagon is 6 cm. The longest side in the ratio is CD, which is 2x. Therefore, we have:
2x=6
From this, we can solve for x:
x=62=3
Now that we have x, we can find the lengths of all the sides:
- AB = √2×3=3√2 cm
- BC = 1×3=3 cm
- CD = 2×3=6 cm
- DE = 1×3=3 cm
- EA = √2×3=3√2 cm
Since angle A is 90 degrees, triangle ABE is a right triangle. The area of triangle ABE can be calculated using the formula:
Area=12×base×height
Here, both the base (AB) and height (EA) are equal to 3√2:
AreaABE=12×3√2×3√2=12×9×2=9 cm2
Next, we can find the area of rectangle BCDE. The length is CD = 6 cm and the breadth is BC = 3 cm:
AreaBCDE=length×breadth=6×3=18 cm2
Finally, we can find the total area of the pentagon by adding the areas of triangle ABE and rectangle BCDE:
Total Area=AreaABE+AreaBCDE=9+18=27 cm2
The area of pentagon ABCDE is 27 cm2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In ΔABC,AB=a−b,AC=√a2+b2 and BC=√2ab, then find angle B.
A60∘B30∘C90∘D45∘ABCDE is a regular pentagon with sides of length 6 cm. CD is also a side of a regular polygon with n sides. Given that ∠EDF=90∘, find n.
 A18∘B10∘C20∘D12∘
A18∘B10∘C20∘D12∘The sides of a triangle are in the ratio 1:√3:2 then the angles of the triangle are in the ratio
A1:3:5B2:3:4C3:2:1D1:2:3
The base of a right prism is a pentagon whose sides are in the raio 1:√2:√2:1:2 and its height is 10 cm. If the longest side of the base be 6 cm, the volume of the prism is
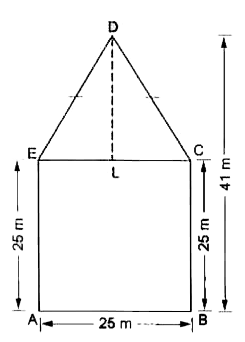
View SolutionIn the given figure ABCDE is a pentagonal park in which DE = DC, AB = BC = CE = EA = 25 m and its total height is 41 m. Find the area of the park.
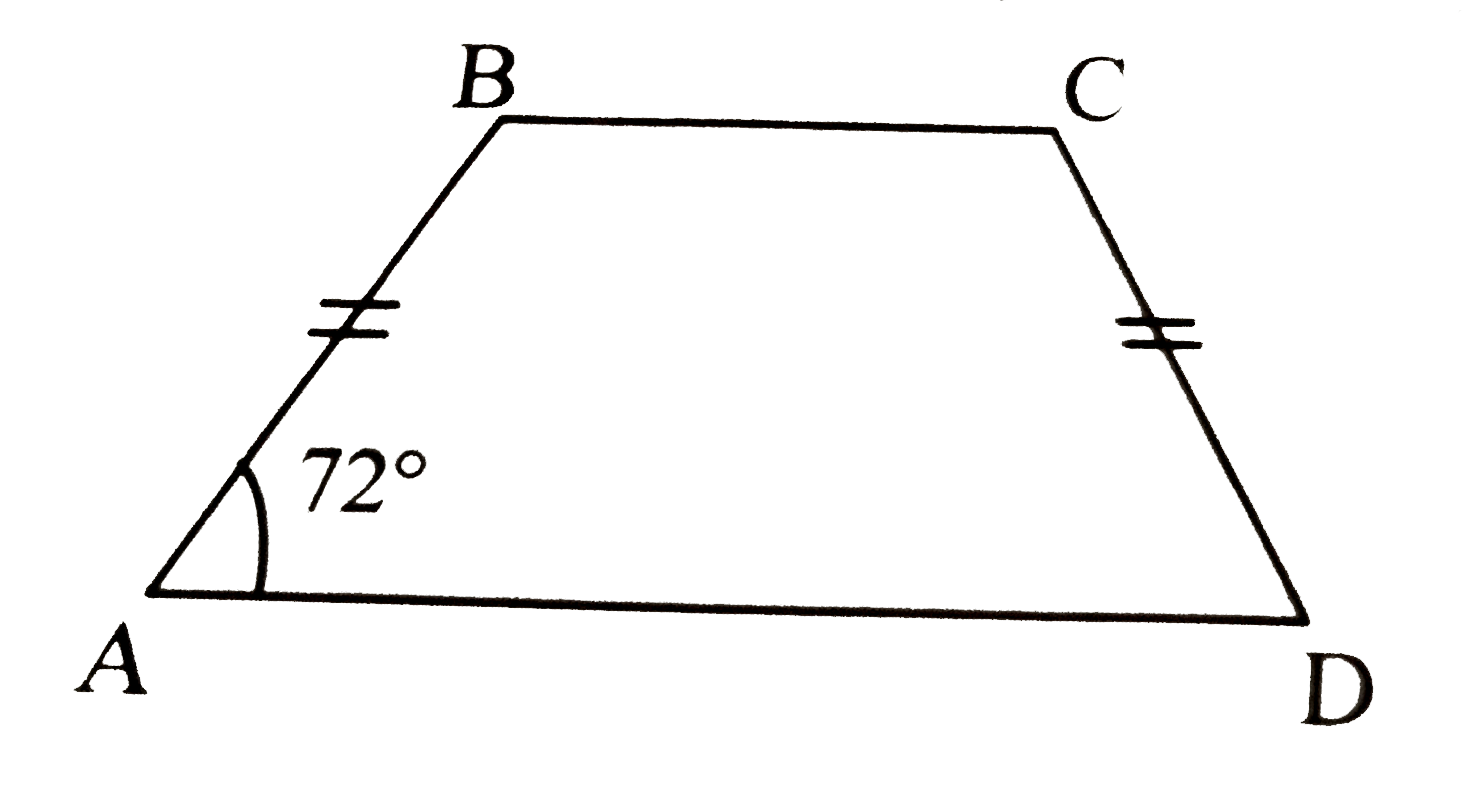
View SolutionIn trapezium ABCD, side BC ∣∣ side AD, side AB ≅ side DC. If ∠A=72∘ , then find the measures of ∠B and ∠D .
View SolutionABCDE is a pentagon prove that −−→AB+−−→BC+−−→CD+−−→DE+−−→EA=→0
View SolutionIf the ratio of angles of ΔABC is 1:2:3, find the ratio of its sides.
View Solution