A uniform disc of radius r and mass m is free to rotate on a frictionless pivot through point P on its rim as shown in Fig. The disc is at rest and is released from the position (1). (i) What is the speed of the centre of mass when the disc reaches the position (2). (ii) Also rind the speed of the lowest point on the disc in the dashed position.

mgh=(1/2)Iω2,I=ml2,I=ml2/3,l=1/2,ω=√6g,α=τ/l=mg×(1/4)(m/12)=3g
Topper's Solved these Questions
Similar Questions
What will be the position of centre of mass of a half disc shown ?
 .
.
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

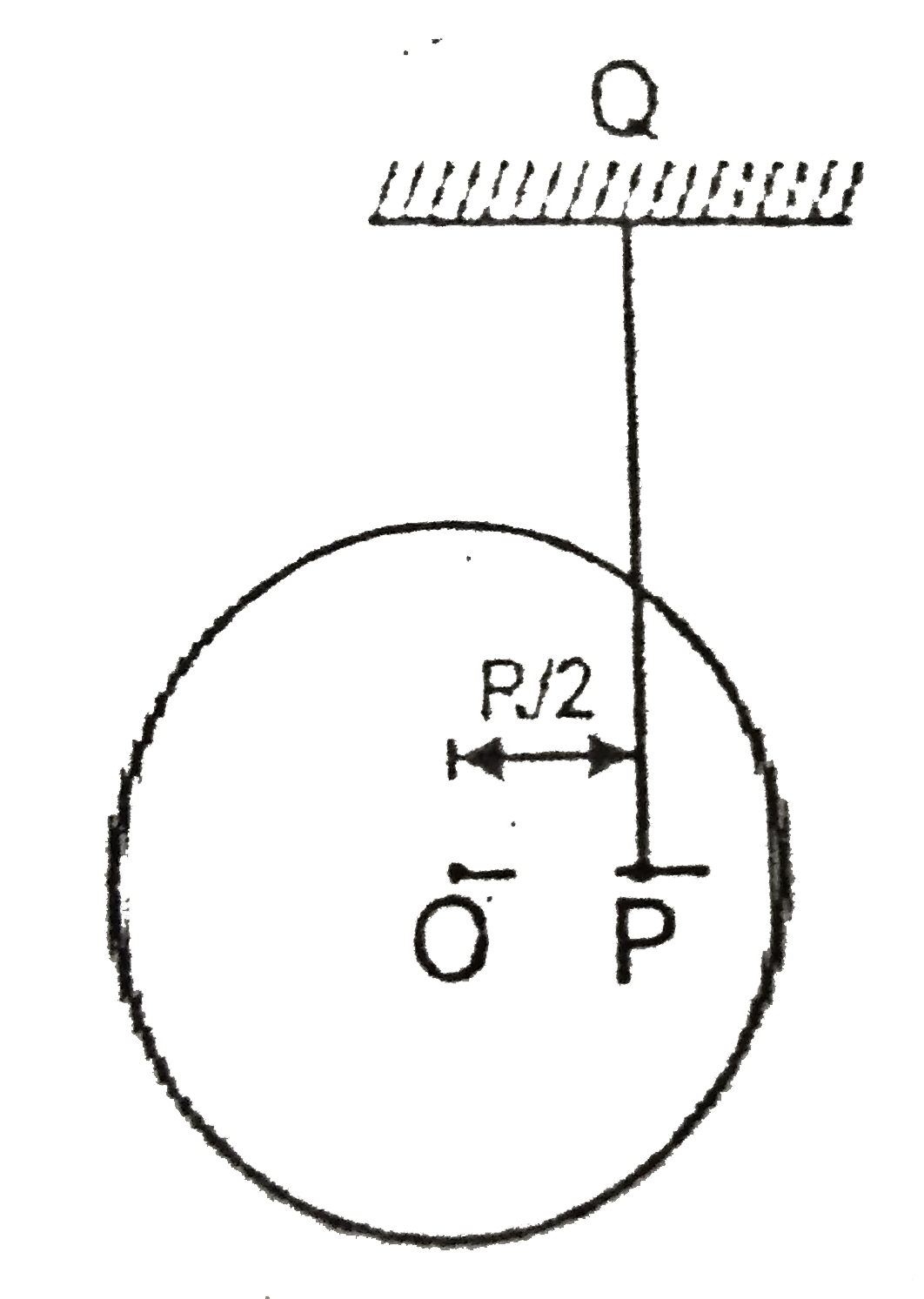
View SolutionA uniform disc of mass M and radius R is released from the shown position . PQ is s tring , OP is a horizontal line , O is the centre of the disc and distance OP is R/2. The tension in the string just after the disc is released will be :
View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionA uniform disc of mass M, radius R is attached to a frictionless horizontal axis. Its rim is wound with a light string and a tension T is applied to it, the angular acceleration will be?
View Solution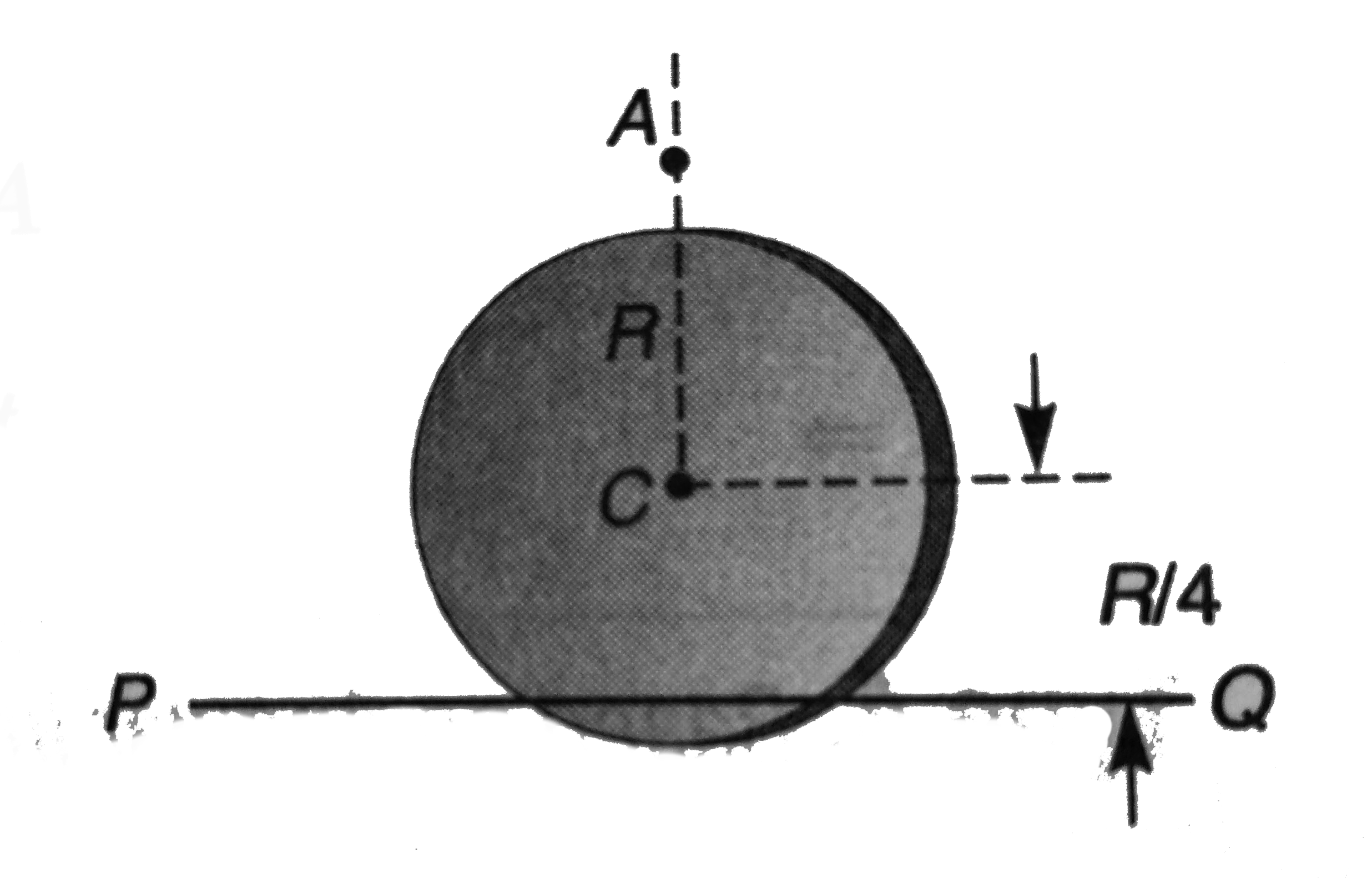
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is

View Solution
