A rectangular tube of uniform cross section has three liquids of densities ρ1,ρ2 and ρ3. Each liquid column has length l equal to length of sides of the equilateral triangle. Find the length x of the liquid of density ρ1 in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

The correct Answer is:x=(ρ2−ρ1l2ρ2=(ρ1+ρ3)
Let us consider two points 1 and 2 in the horizontal limb. Pressure at 1 is P1 and ρ1gh1+ρ2gh2
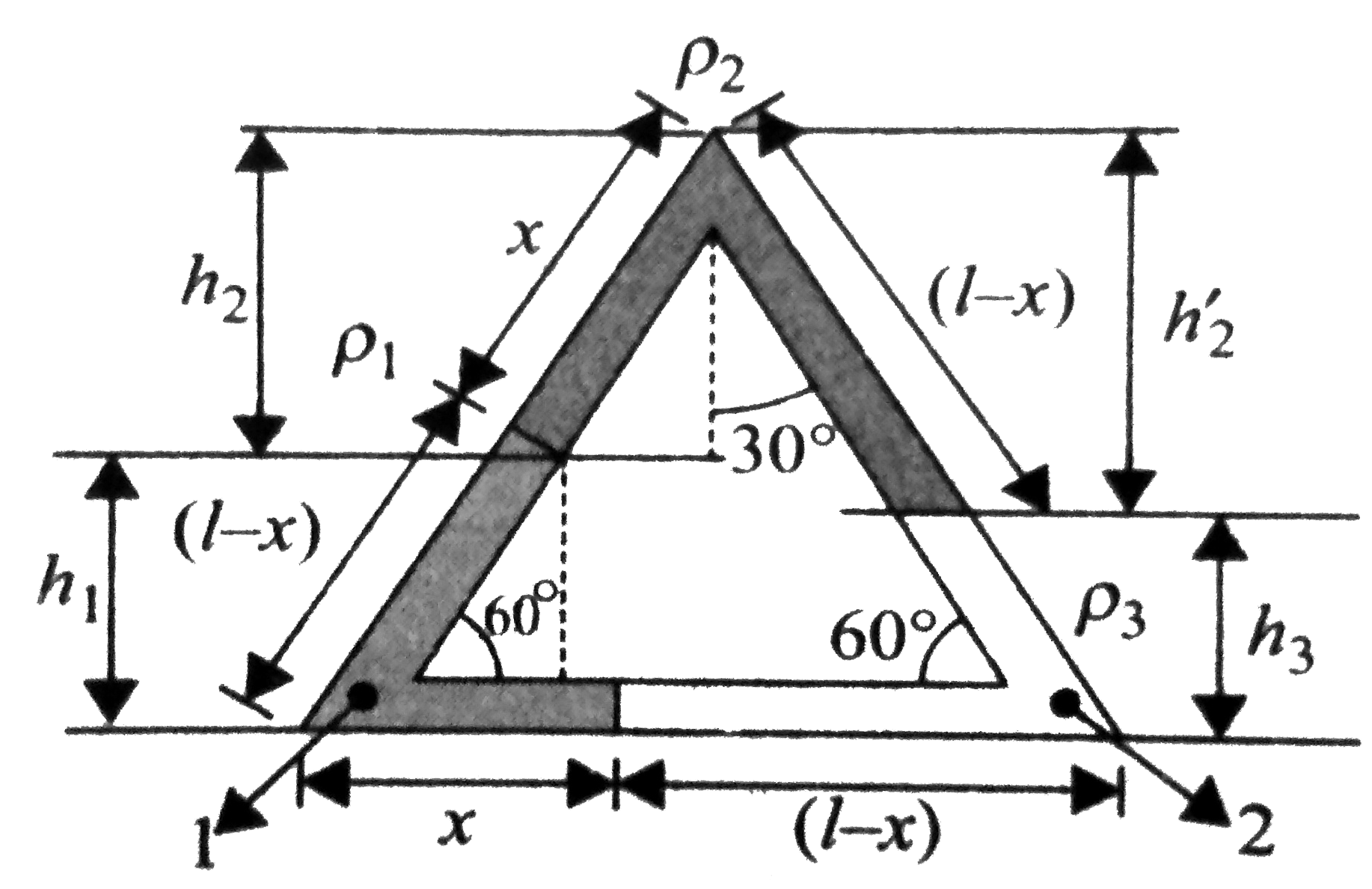
pressure at 2 is P2=ρgh′2=ρ3gh3
Since P1=P2 for non accelerating liquid, we have
ρ1h1+ρ2h2=ρ2h′2+ρ3h3
Substituting h1=h′2(l−x)sin60∘ and h2−h3=xsin60∘, we have
x=(ρ2−ρ1)l2ρ2−(ρ1+ρ3)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

View SolutionFind time period of liquid column of length l in the shown tube.

View SolutionFig shows the same block of wood floating in three different liquids A,B and C of densities ρ1,ρ2 and ρ3 respectively. Which liquid has the highest density? Give reason for your answer.

View SolutionThree liquids having densities ρ1,ρ2,ρ3 are filled in a U-tube. Length of each liquid column is equal to I, ρ1>ρ2>ρ3 and liquids remain at rest (relative to the tube) in the position shown in the figure. It is possible that

View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
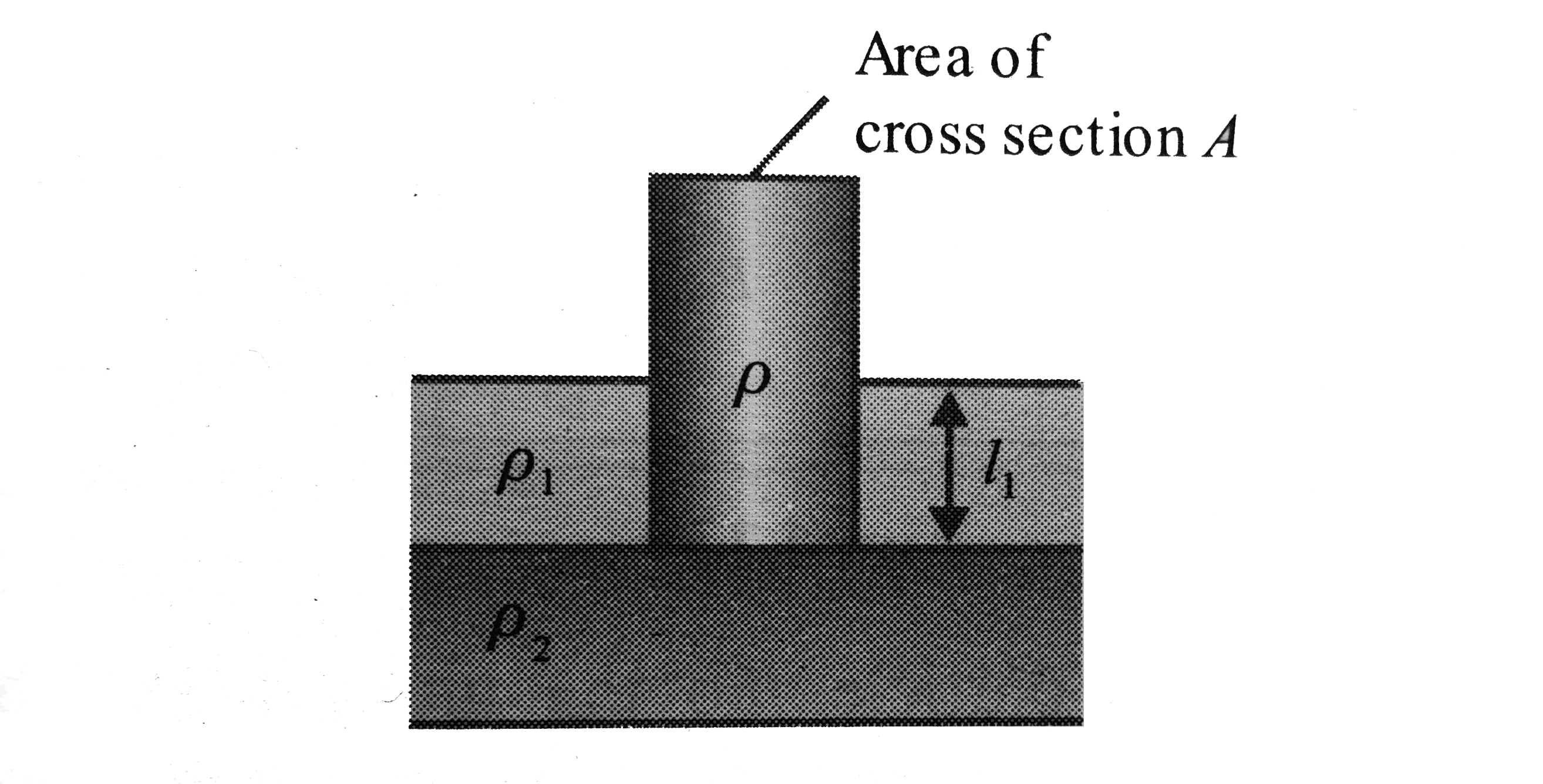
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
View Solution_E01_053_Q01.png)
There are three different liquids, with densities ρ1,ρ2 and ρ3 in a U-shaped container as shown in the picture the lengths shown are H1=15cm and H2=10cm which of the following equations gives the correct relation between the densities of the fluids in the container?
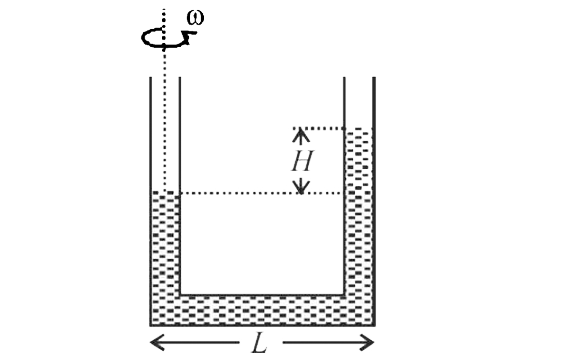
View SolutionA U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
View SolutionA V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrum the level of liquid in both limds of tube. Find the angular frequency of small oscillation of liquid.

View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View Solution
