A steering wheel of diameter 0.5m is rotated anticlockwise by applying two forces each of magnitude 5N. Draw a diagram to show the application of forces and calculate the moment of the force applied.
To solve the problem, we need to calculate the moment of the force applied to the steering wheel when two forces are applied. Let's break down the steps:
Step 1: Understand the Problem
We have a steering wheel with a diameter of 0.5 meters. We need to calculate the moment of the forces applied to it.
Step 2: Calculate the Radius
The radius of the steering wheel can be calculated using the formula:
Radius=Diameter2
Given that the diameter is 0.5 m:
Radius=0.5m2=0.25m
Step 3: Draw the Diagram
Draw a circle to represent the steering wheel. Mark the center of the wheel and label it as point O. Draw two arrows representing the forces applied at points A and B on the circumference of the wheel, both directed anticlockwise. Each arrow should be labeled with the force magnitude of 5 N.
Step 4: Calculate the Moment of Force for Point A
The moment of force (also known as torque) can be calculated using the formula:
Moment=Force×Perpendicular Distance
For point A:
- Force = 5 N
- Perpendicular Distance = Radius = 0.25 m
Moment at A=5N×0.25m=1.25N m
Step 5: Calculate the Moment of Force for Point B
Since the forces are applied symmetrically, the moment at point B will be the same as at point A:
Moment at B=5N×0.25m=1.25N m
Step 6: Calculate the Total Moment
The total moment of the forces applied to the steering wheel is the sum of the moments at points A and B:
Total Moment=Moment at A+Moment at B=1.25N m+1.25N m=2.5N m
Final Answer
The total moment of the forces applied to the steering wheel is 2.5 N m.
---
We have a steering wheel with a diameter of 0.5 meters. We need to calculate the moment of the forces applied to it.
The radius of the steering wheel can be calculated using the formula:
Radius=Diameter2
Given that the diameter is 0.5 m:
Radius=0.5m2=0.25m
Draw a circle to represent the steering wheel. Mark the center of the wheel and label it as point O. Draw two arrows representing the forces applied at points A and B on the circumference of the wheel, both directed anticlockwise. Each arrow should be labeled with the force magnitude of 5 N.
The moment of force (also known as torque) can be calculated using the formula:
Moment=Force×Perpendicular Distance
For point A:
- Force = 5 N
- Perpendicular Distance = Radius = 0.25 m
Moment at A=5N×0.25m=1.25N m
Since the forces are applied symmetrically, the moment at point B will be the same as at point A:
Moment at B=5N×0.25m=1.25N m
The total moment of the forces applied to the steering wheel is the sum of the moments at points A and B:
Total Moment=Moment at A+Moment at B=1.25N m+1.25N m=2.5N m
The total moment of the forces applied to the steering wheel is 2.5 N m.
Topper's Solved these Questions
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1B
11 Videos
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1(B) Multiple choice questions
2 Videos
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1(A) Multiple choice questions
2 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
- HOUSEHOLD CIRCUITS BOOK - ICSECHAPTER - HOUSEHOLD CIRCUITS EXERCISE - EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
A wooden block is placed on a table top. Name the forces acting on the block and draw a neat and labelled diagram to show the point of application and direction of these forces.
View SolutionA body is pivoted at a point. A force of 10N is applied at a distance of 30cm from the pivot. Calculate the moment of force about the pivot.
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
In Fig. 1.17 a roller of diameter 0.4m is raised on the pavement XY by forces F1andF2 each of magnitude 10N. Compare the torques produced by the two forces.
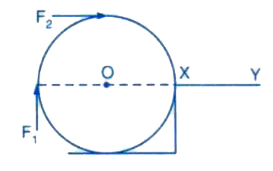
View SolutionTwo forces each of magnitude 5 N are applied in opposite directions at the ends of a uniform nod of length 0.5 m. Draw diagram of the arrangement and find the total moment of the two forces.
View SolutionTwo forces of magnitude 3N and 4N respectively are acting on a body. Calculate the resultant force if the angle between them is
0∘
View SolutionA block is applied two forces of magnitude 5N each. One force is acting towards East and the other acting along 60∘ North of East. The resultant of the two forces (in N) is of magnitude :-
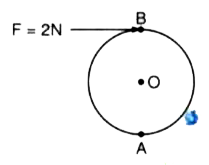
View SolutionA wheel of diameter 2m is shown in Fig 1.28 with axle at O. At force F= 2N is applied at B in the direction shown in figure, Calculate the moment of force about (i) the centre O, and (ii) the point A.
View SolutionA ball of mass 0.2 kg is thrown vertically upwards by applying a force by hand. If the hand moves 0.2 m while applying the force and the ball goes upto 2 m height further, find the magnitude of the force. (Consider g=10m/s2).
View SolutionA ball of mass 0.2 kg is thrown vertically upwards by applying a force by hand. If the hand moves 0.2 m while applying the force and the ball goes upto 2 m height further, find the magnitude of the force. (Consider g=10m/s2).
View Solution
