A fixed pulley is driven by a 100 kg mass falling at a rate of 8⋅0m in 4⋅0s. It lifts a load of 75⋅0 kgf. Calculate
(a) The power input to the pulley taking the force of gravity on 1 kg as 10 N.
(b) the efficiency of the pulley, and
(c) The height to which the load is raised in 4⋅0s.
The correct Answer is:(a) 2000W, (b) 0⋅75, (c) c 8⋅0m.
Let's solve the problem step by step.
Given Data:
- Mass of falling object (effort) = 100 kg
- Rate of fall = 8 m in 4 s
- Load lifted = 75 kgf
- Gravitational force (g) = 10 N/kg
Step 1: Calculate the Force of the Falling Mass
The force exerted by the falling mass can be calculated using the formula:
Force=mass×gravity
Force=100kg×10N/kg=1000N
Step 2: Calculate the Power Input to the Pulley
Power input can be calculated using the formula:
Power=Effort×DistanceTime
Where:
- Effort = 1000 N (from Step 1)
- Distance = 8 m (given)
- Time = 4 s (given)
Now substituting the values:
Power=1000N×8m4s
Power=8000N m4s=2000W
Step 3: Calculate the Efficiency of the Pulley
Efficiency can be calculated using the formula:
Efficiency=Mechanical AdvantageVelocity Ratio×100%
Step 3.1: Calculate Mechanical Advantage (MA)
Mechanical Advantage is given by:
MA=LoadEffort
Where:
- Load = 75 kgf = 75 kg × 10 N/kg = 750 N
- Effort = 1000 N (from Step 1)
Now substituting the values:
MA=750N1000N=0.75
Step 3.2: Calculate Velocity Ratio (VR)
For a fixed pulley, the velocity ratio is:
VR=1
Step 3.3: Calculate Efficiency
Now substituting the values into the efficiency formula:
Efficiency=0.751×100%=75%
Step 4: Calculate the Height to Which the Load is Raised
Since the velocity ratio is 1, the distance moved by the load is equal to the distance moved by the effort.
- Distance moved by effort = 8 m (given)
Thus, the height to which the load is raised is:
Height=8m
Final Answers:
(a) Power input to the pulley = 2000 W
(b) Efficiency of the pulley = 75%
(c) Height to which the load is raised = 8 m
- Mass of falling object (effort) = 100 kg
- Rate of fall = 8 m in 4 s
- Load lifted = 75 kgf
- Gravitational force (g) = 10 N/kg
The force exerted by the falling mass can be calculated using the formula:
Force=mass×gravity
Force=100kg×10N/kg=1000N
Power input can be calculated using the formula:
Power=Effort×DistanceTime
Where:
- Effort = 1000 N (from Step 1)
- Distance = 8 m (given)
- Time = 4 s (given)
Power=1000N×8m4s
Power=8000N m4s=2000W
Efficiency can be calculated using the formula:
Efficiency=Mechanical AdvantageVelocity Ratio×100%
Mechanical Advantage is given by:
MA=LoadEffort
Where:
- Load = 75 kgf = 75 kg × 10 N/kg = 750 N
- Effort = 1000 N (from Step 1)
MA=750N1000N=0.75
For a fixed pulley, the velocity ratio is:
VR=1
Now substituting the values into the efficiency formula:
Efficiency=0.751×100%=75%
Since the velocity ratio is 1, the distance moved by the load is equal to the distance moved by the effort.
- Distance moved by effort = 8 m (given)
Height=8m
(a) Power input to the pulley = 2000 W
(b) Efficiency of the pulley = 75%
(c) Height to which the load is raised = 8 m
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MACHINESEXERCISE - EXERCISE-3(B) MULTIPLE CHOICE TYPE3videos
MACHINES
- BOOK - ICSECHAPTER - HOUSEHOLD CIRCUITS EXERCISE - EXERCISE -9(B) (MULTIPLE CHOICE TYPE)2videos
HOUSEHOLD CIRCUITS
- BOOK - ICSECHAPTER - QUESTION PAPER 2022 TERM 1EXERCISE - MULTIPLE CHOICE QUESTIONS40videos
QUESTION PAPER 2022 TERM 1
Similar Questions
A machine is driven by a 100 kg mass that falls 8m in 4⋅0s. it lifts a load of mass 500 kg vertically upwards. Taking g=10ms−2. Calculate:
(a) the force exerted by the falling mass.
(b) the work done by the falling mass in its displacement by 8⋅0m.
(c) the power input to the machine.
(d) the power output of the machine if its efficiency is 60%, and
(e) the work done by the machine is 4⋅0s.View SolutionA pulley system with a velocity ratio 4 is used to lift a load of 300 kgf to a vertical height of 10 m by applying an effort of 100 kgf downwards.
ind the efficiency of the pulley system and the work done by the effort.View SolutionThe mass of a body is 20-0 kg. Taking the pull of gravity on mass 1 kg equal to 10 N, express the weight of the body in kgf .
View SolutionThe mass of a body is 20-0 kg. Taking the pull of gravity on mass 1 kg equal to 10 N, express the weight of the body in newton .
View SolutionA way pulse is travelling on a string of linear mass density 6.4×10−3kgm−1 under a load of 80kgf. Calculate the time taken by the pulse to traverse the string, if its length is 0.7m.
View SolutionA pulley system with V.R. = 4 is used to lift a load of 175 kgf through a vertical height of 15 m. The effort required is 50 kgf in the downward direction. (g=10Nkg−1)
Calculate :
Efficiency of the pulley system.View SolutionA boy mass 40 kg climbs up the stairs and reaches the roof at a height 8 m in 5 s. Calculate :
(i)the force of gravity acting the boy .
(ii) the work done by against the force of gravity .
(iii)the power spent by the boy .
(Take g=10 m S−2)View SolutionA pulley system with a velocity ratio of 4 is used to lift a load of 150 kgf through a vertical height of 20 m. the effort required is 50 kgf in downward direction. Calculate:
(a) the distance moved by the effort.
(b) the work done by the effort.
(c) the mechanical advantage.
(d) the efficiency of the pulley system, and
(e) the total number of pulleys and the number of pulleys in each block.
(g=10N kg−1).View SolutionThe adjacent Figure shows a fixed pulley used by a boy to lift a load of 400 N through a vertical height of 5 m in 10 s. the effort applied by the boy on the other end of the rope is 480 N.
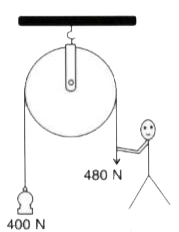
(a) What is the velocity ratio of the pulley ?
(b) What is the mechanical advantage ?
(c) Calculate the efficiency of the pully.
(d) Why is the efficiency of the pulley not 100% ?
(e) What is the energy gained by the load in 10 s?
(f) How much power was developed by the boy in raising the load ?
(g) The boy has to apply an effort which is greater than the load he is lifting. what is the justification for using the pulley ?View SolutionA pulley system with a velocity ratio 4 is used to lift a load of 300 kgf to a vertical height of 10 m by applying an effort of 100 kgf downwards.
Draw the arrangement of pulley showing the load (L), effort (E) and tension (T) in each strand.View Solution

