A coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
The correct Answer is:3 cm
To solve the problem of how much the coin appears to be raised when viewed from above the water, we can follow these steps:
1. Identify the Given Values:
- Actual depth of the coin (dA) = 12 cm
- Refractive index of water (n) = 4/3
2. Use the Formula for Apparent Depth:
The formula for apparent depth (dA') when light passes from a medium of higher refractive index to a medium of lower refractive index is given by:
dA′=dAn
Substituting the known values:
dA′=12 cm4/3
3. Calculate the Apparent Depth:
To perform the division, we can multiply by the reciprocal of the refractive index:
dA′=12 cm×34=9 cm
4. Determine the Shift in Position:
The shift (s) in the position of the coin can be calculated using the formula:
s=dA−dA′
Substituting the values we have:
s=12 cm−9 cm=3 cm
5. Conclusion:
The coin appears to be raised by 3 cm when viewed from directly above the water.
Final Answer:
The coin appears to be raised by 3 cm.
---
- Actual depth of the coin (dA) = 12 cm
- Refractive index of water (n) = 4/3
The formula for apparent depth (dA') when light passes from a medium of higher refractive index to a medium of lower refractive index is given by:
dA′=dAn
Substituting the known values:
dA′=12 cm4/3
To perform the division, we can multiply by the reciprocal of the refractive index:
dA′=12 cm×34=9 cm
The shift (s) in the position of the coin can be calculated using the formula:
s=dA−dA′
Substituting the values we have:
s=12 cm−9 cm=3 cm
The coin appears to be raised by 3 cm when viewed from directly above the water.
The coin appears to be raised by 3 cm.
Topper's Solved these Questions
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(D)
30 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(D) MULTIPLE CHOICE TYPE
3 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(C) MULTIPLE CHOICE TYPE
2 Videos
- REFRACTION OF LIGHTBOOK - ICSECHAPTER - REFRACTION OF LIGHTEXERCISE - DIAGRAM BASED MCQ:
5 Videos
- REFRACTION THROUGH A LENS BOOK - ICSECHAPTER - REFRACTION THROUGH A LENS EXERCISE - EXERCISE-5(D) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
A coin is placed at the bottom of a glass trough containing water (refractive index = 43 ) up to a height 20 cm. At what depth it will appear when it is viewed from air, vertically above the coin. Draw a suitable ray diagram in support of your answer.
View SolutionA coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View Solution
Knowledge Check
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
A2.6m2B3.6m2C4.2m2D5.8m2
A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
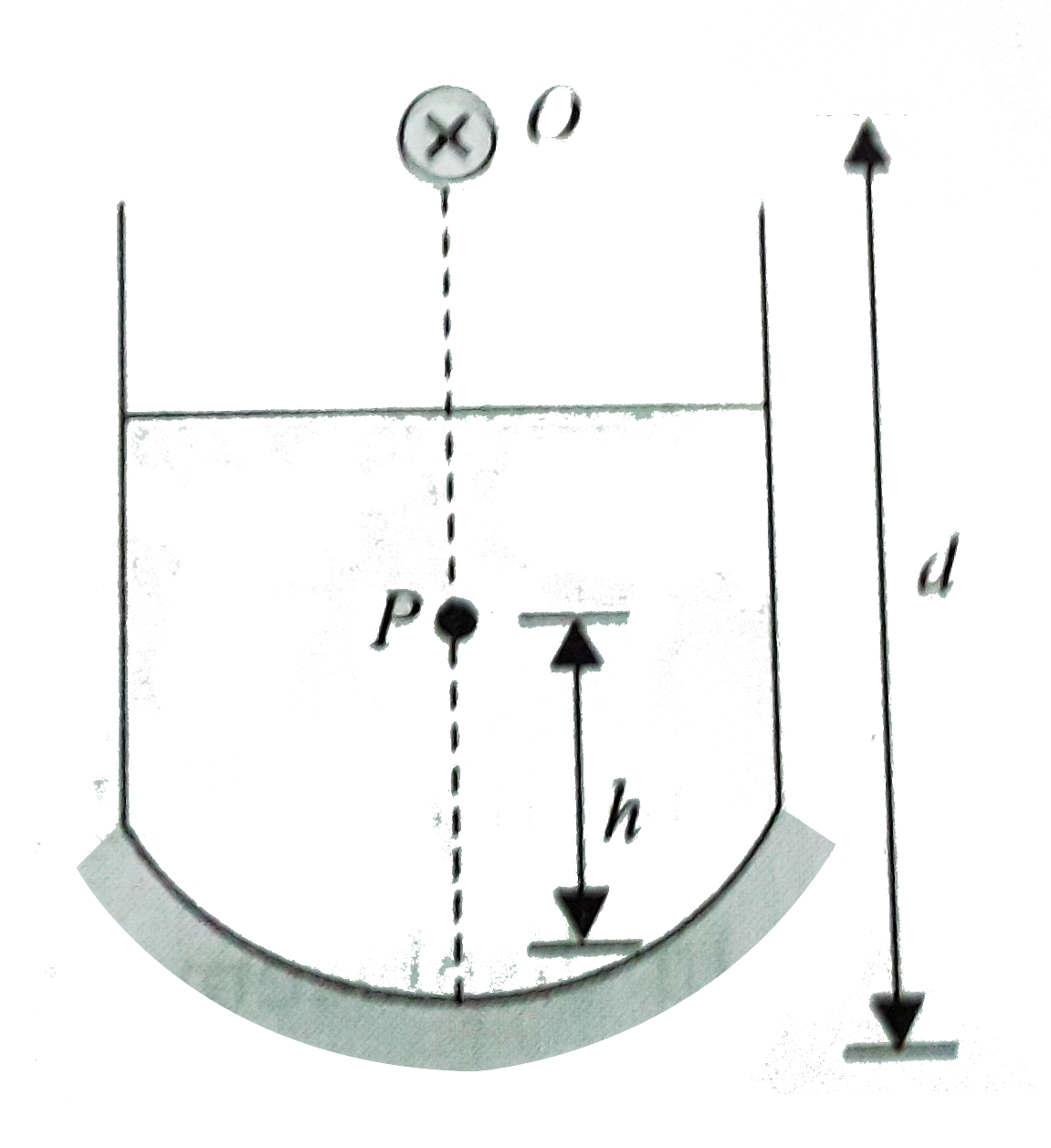
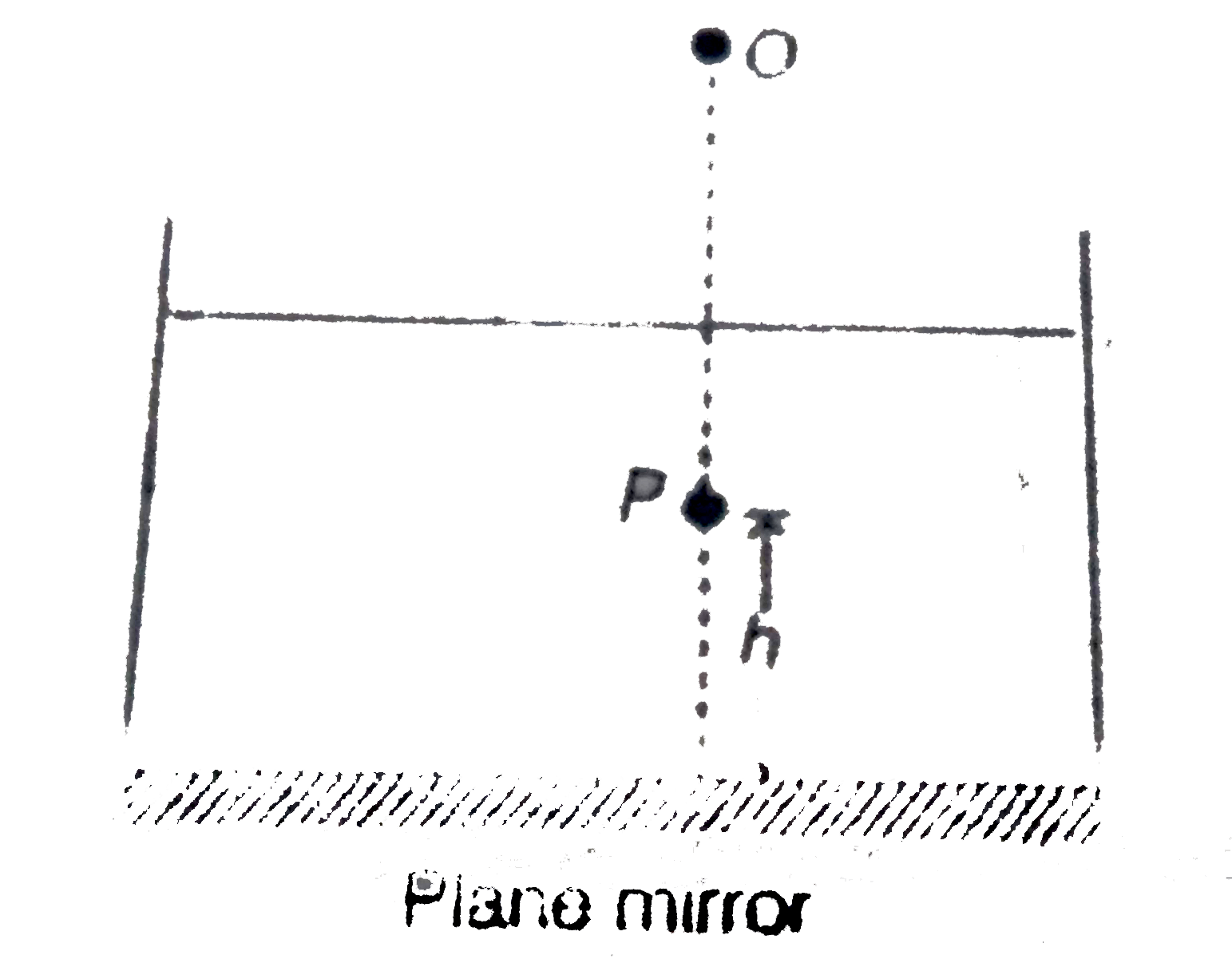
View SolutionConsider the situation shown in figure. A plane mirror is fixed at a height h above the bottom of a beaker containing water (refractive index μ) up of a bottom formed by the mirror.Find the position of the image of bottom formed by the mirror.

View SolutionA plane mirror is fixed at the bottom of a tank containing water. A small object is kept at a height of 24 cm from the bottom and is viewed from a point vertically above it. The distance between the object and the image in the mirror as appears to the person is
View SolutionA parallel sided block of glass of refractive index 1.5 which is 36 mm thick rests on the floor of a tank which is filled with water (refractive index = 4/3). The difference between apparent depth of floor at A and B when seen from vertically above is equal to

View SolutionA plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observer observes P and its image in the mirror. The apparent distance between two will be
View SolutionA small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View Solution
