In ΔABC, AD divides BC in thr ratio m:n. Show that Area(ΔABD)Area(ΔADC)=mn
Step by step video & image solution for In DeltaABC, AD divides BC in thr ratio m:n. Show that ( "Area" (DeltaABD))/( "Area" (DeltaADC))=(m)/(n) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(A)
36 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
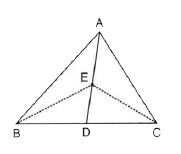
In the given figure, AD is median of ΔABC and E is any point on median AD. Prove that Area (ΔABE) = Area (ΔACE)
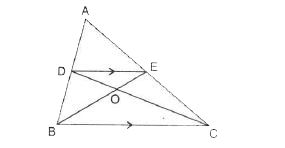
View SolutionIn the following figure, DE is parallel to BC. Show that :
(i) Area(ΔADC)=Area(ΔAEB)
(ii) Area(ΔBOD)=Area(ΔCOE).
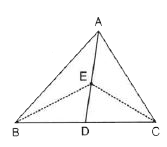
View SolutionIn the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).
View SolutionIn the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).

View SolutionIn a ΔABC,D in mid-point of BC, AD is produced upto E so that DE=AD, prove that :
(i) ΔABD and ΔECD are congruent (ii) AB=EC
(iii) AB is parallel to EC.
View SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 4. Find the ratio :

Area of ΔDEFArea ofΔBFC
View SolutionThe base BC of triangle ABC is divided at D so that BD = 12 DC.
Prove that area of ΔABD=13 of the area of ΔABC.
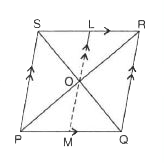
View SolutionIn the given figure, diagonals PR and QS of thr parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :
(i) 2Area(ΔPOS)=Area(//gmPMLS)
(ii) Area(ΔPOS)+Area(ΔQOR)
=12Area(//gmPQRS)
(iii) Area(ΔPOS)+Area(ΔQOR)
=Area(ΔPOQ)+Area(tΔSOR)
View SolutionABCD is a trapezium with AB//DC. A line parallel to AC intersects Ab at point M and BC at point N. Prove that :
area ofΔADM=area ofΔACN.
View SolutionIn ΔABC, a point P on BC divided BC in the ratio 1:1. what is the line segment joining vertex A and P called ?
View Solution
