In the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 4. Find the ratio :

Area of ΔDEFArea ofΔBFC
The correct Answer is:2564
Step by step video, text & image solution for In the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 4. Find the ratio : ("Area of "DeltaDEF)/("Area of"Delta BFC) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(A)48videos
SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)
- BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)17videos
SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)
- BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)10videos
SIMILARITY
- BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )18videos
SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)
Similar Questions
In the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 3. Find the ratio :
ADAB and then DEBCView SolutionIn the given triangle PQR, LM is parallel to QR and PM : MR = 3: 4.

Calculate the value of ratio :
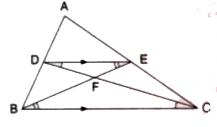
Area of ΔLMNArea of ΔMNRView SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
 View Solution
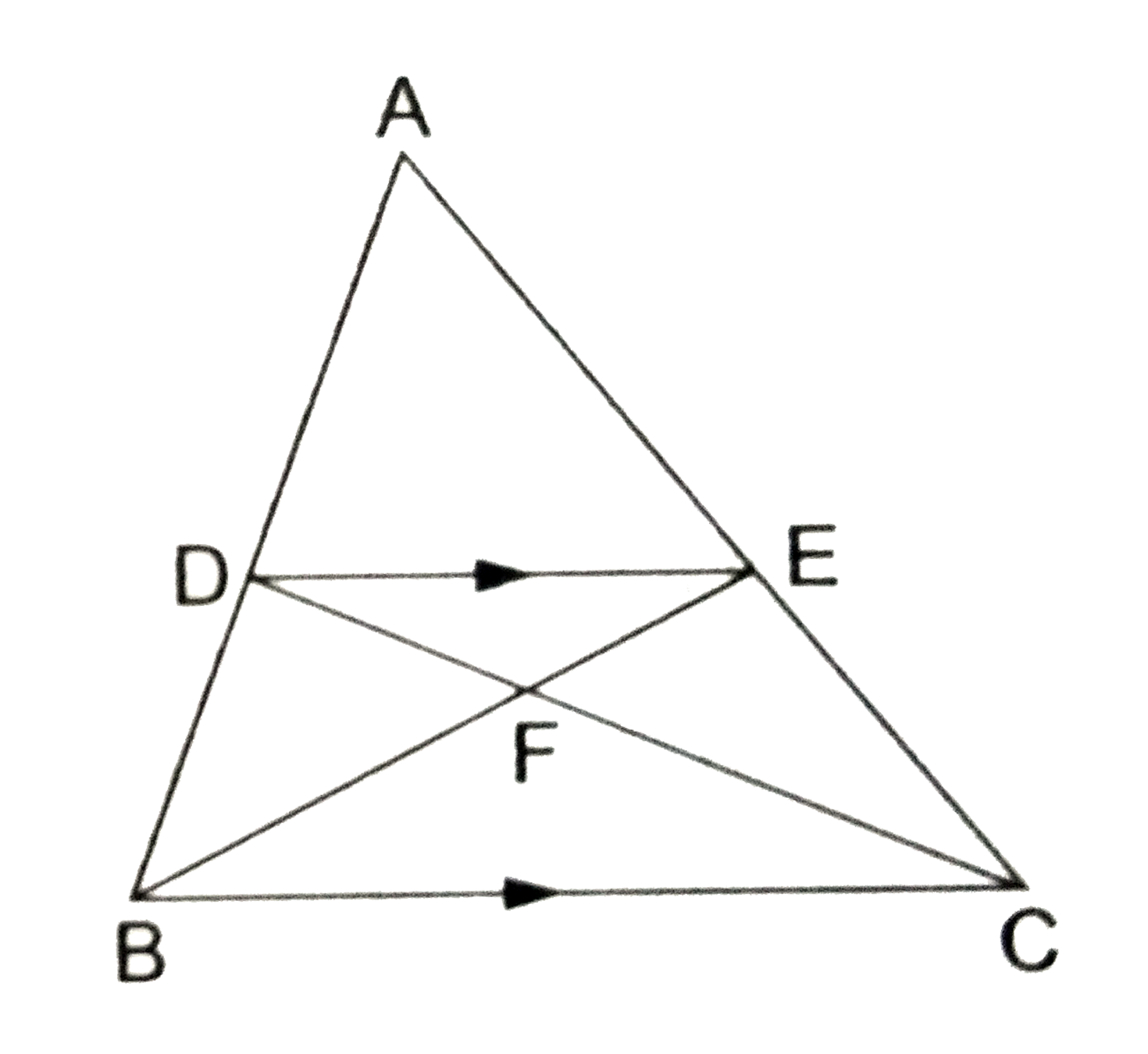
View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

What is the ratio of the areas of ΔDEF and ΔBFC ?View SolutionIn the given figure, DE // BC and AE : EC = 5 : 4. Find :
area of ΔDOE : area of ΔOCB
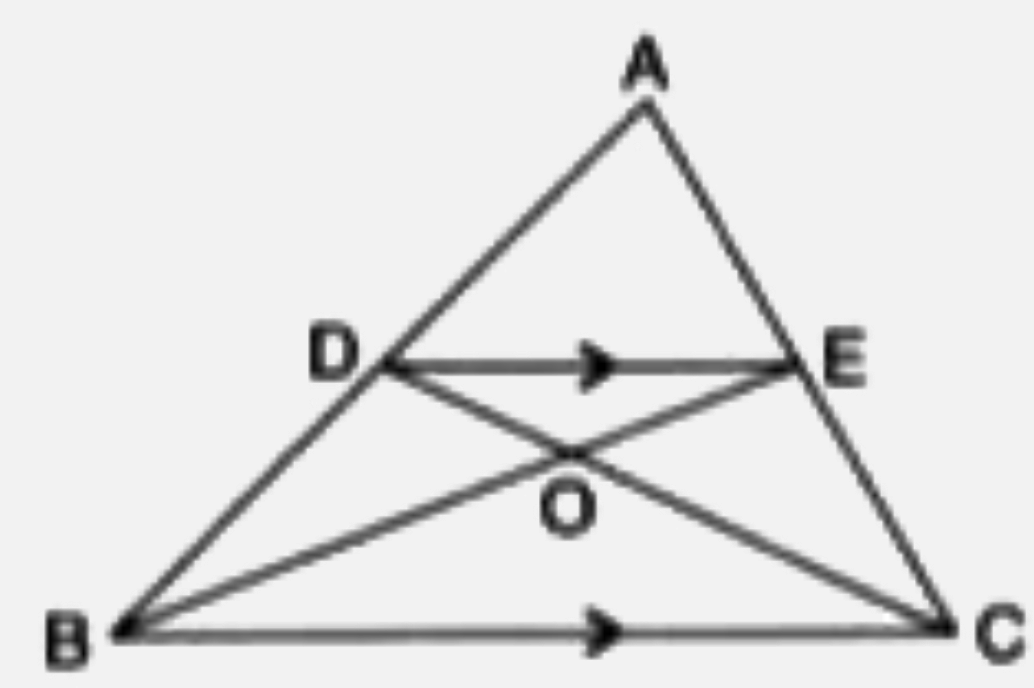 View Solution
View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.

Find the ratio of the area of DetlaADB is to area of ΔCDA.View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

Determine the ratios and ADABView SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
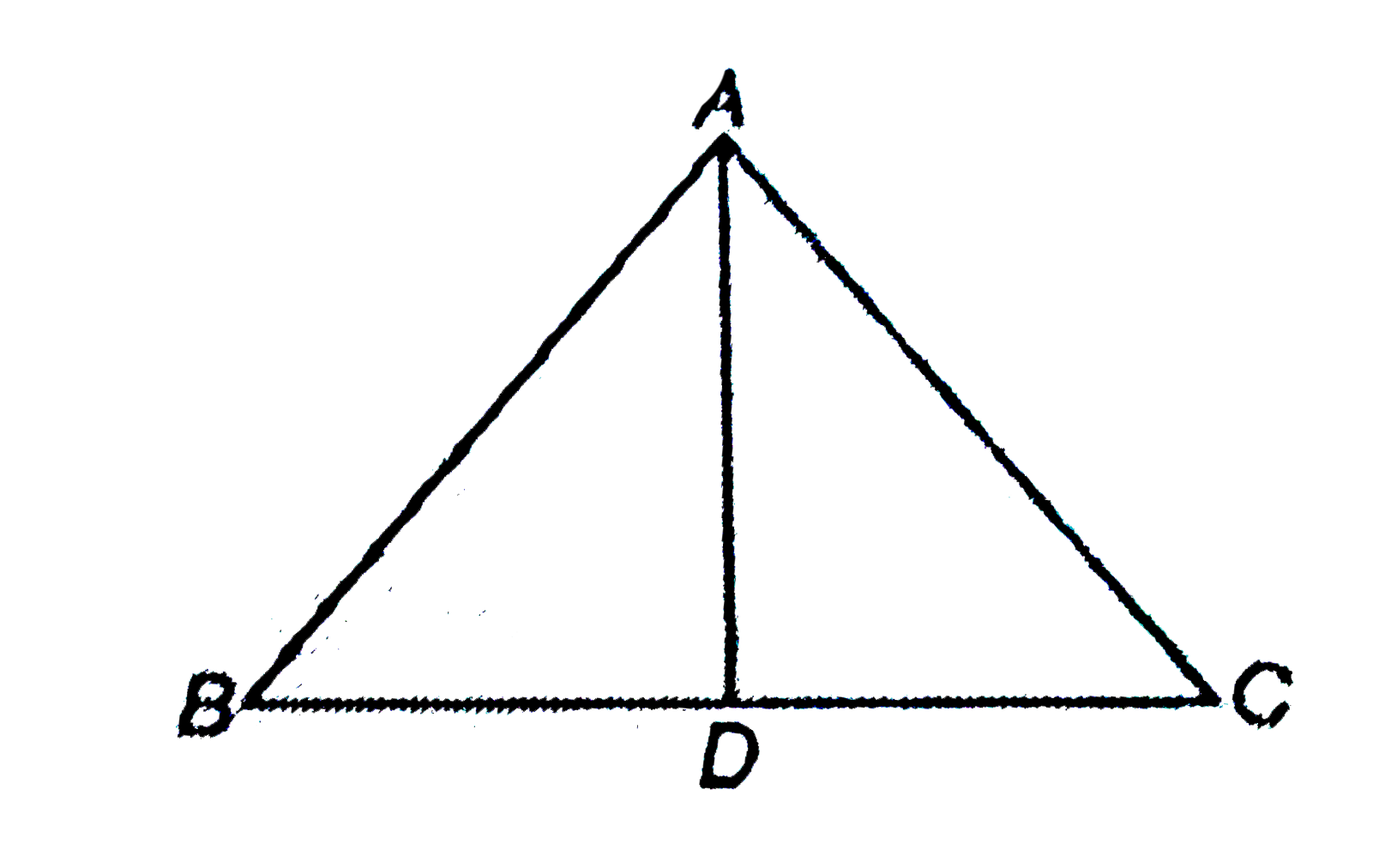 View Solution
View SolutionIn the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangles ABC and BQP are equal.
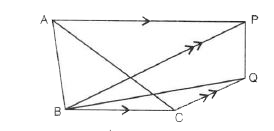 View Solution
View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.
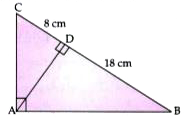
Find the ratio of the area of ΔADB to area of ΔCDA.View Solution

