In the given figure, O is the centre of the circumcircle of △ABC. Tangents at A and C intersect at P. Given angle AOB=140∘ and angle APC=80∘ find the angle BAC.
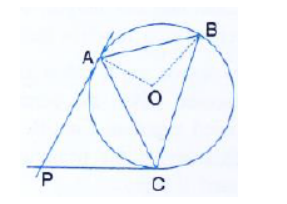
The correct Answer is:∠BAC=60∘
Step by step video & image solution for In the given figure, O is the centre of the circumcircle of triangleABC. Tangents at A and C intersect at P. Given angle AOB=140^(@) and angle APC=80^(@) find the angle BAC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)
42 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)
42 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
In the figure given below O is the centre of the circumcircle of triangle XYZ.
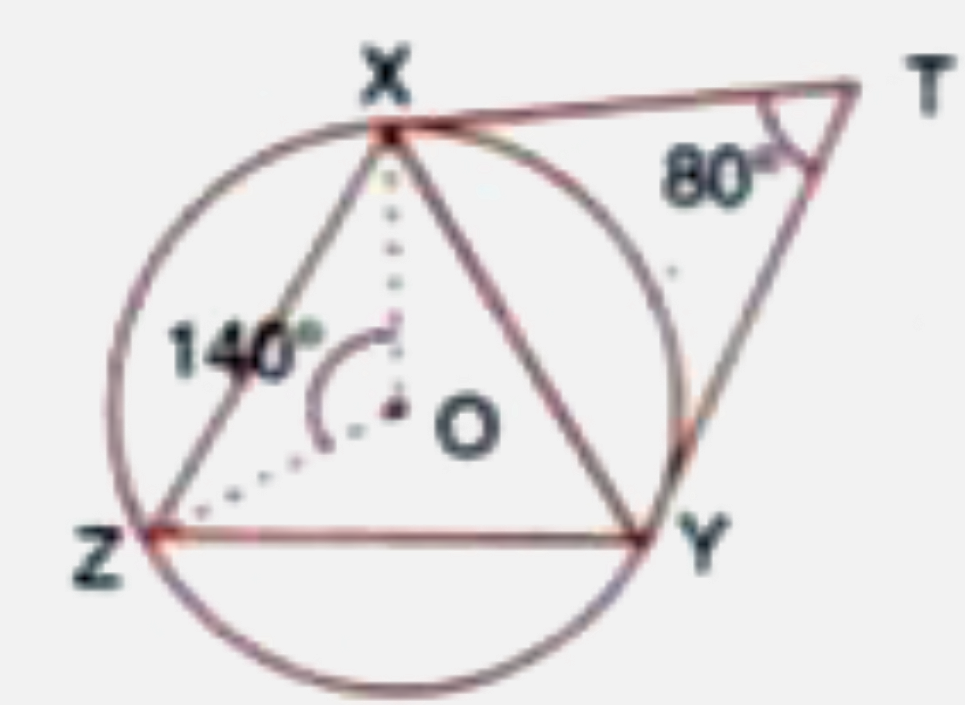
Tangents at X and Y intersect at point T. Given ∠XTY=80∘ and ∠XOZ=140∘, calculate the value of ∠ZXY.
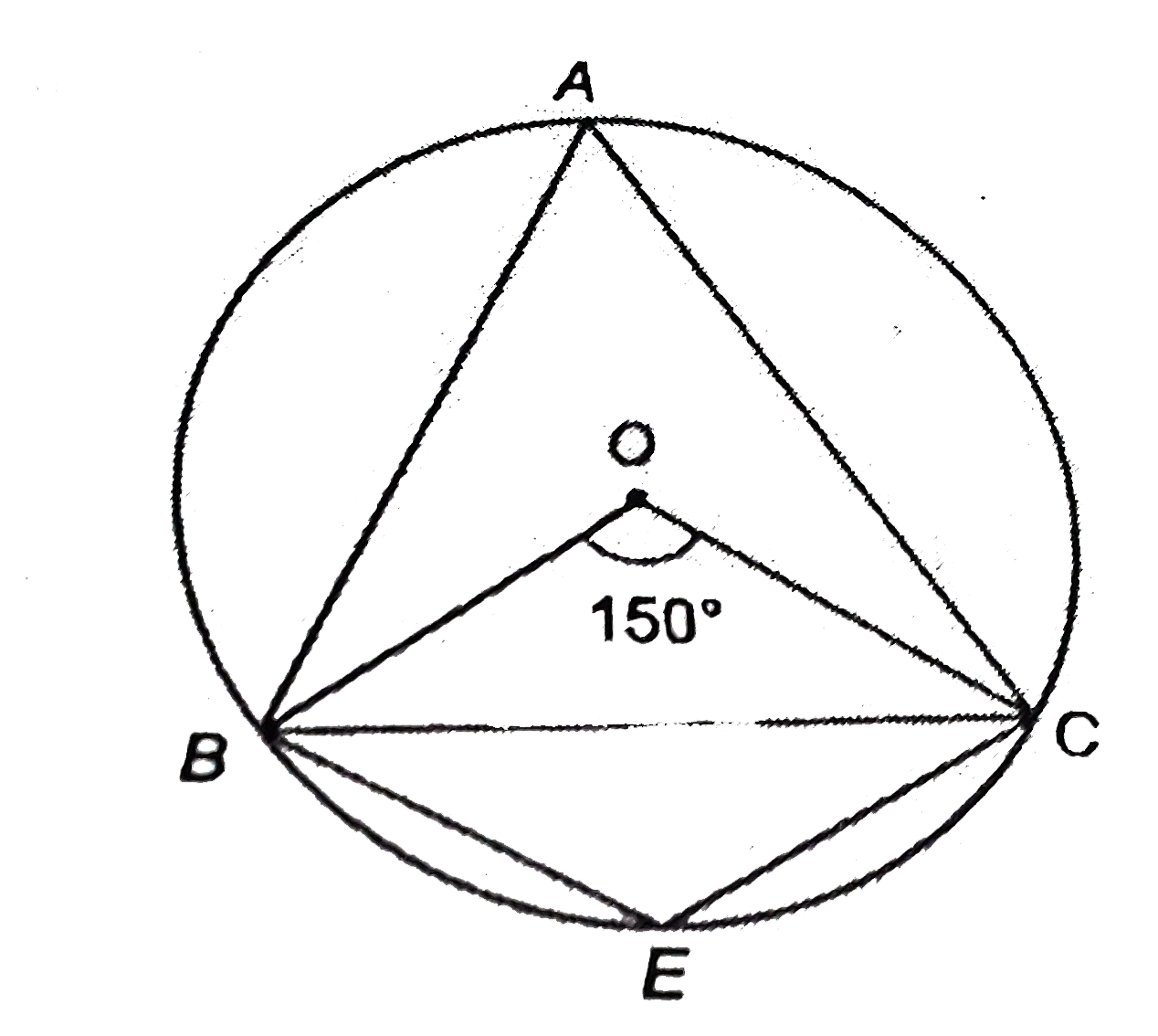
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
View SolutionIn the given figure, find ∠AOB.

View SolutionIn the given figure, find ∠ABC.

View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

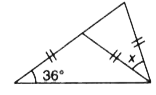
View SolutionUse the given figure to find the angle x.
View SolutionIn the given figure, O is the centre of a circle and ∠ADC=130∘.If ∠BAC=x∘, Find the value of x.

View SolutionIn the given figure ,I is the incentre of triangle ABC . AI produced meets the circumcircle of the triangle ABC at point D. if ∠BAC=50∘and∠ABC=70∘, find :
(i) ∠BCD(ii)∠ICD(iii)∠BIC
(##SEL_RKB_ICSE_MAT_X_C17_E01_015_Q01.png" width="80%">
View SolutionIn the given figure O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO=30∘ find
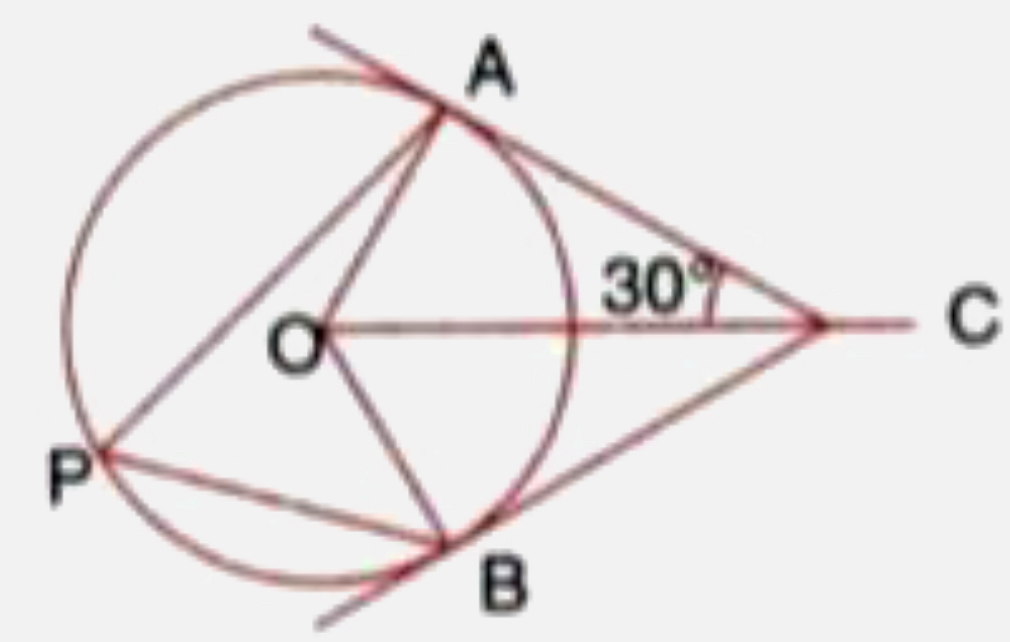
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB
View SolutionIn the given figure, find ∠D and ∠B.

View Solution
