In the given figure , ∠ACE=43∘and∠CAF=62∘, find the values of a,b and c.
The correct Answer is:58∘
To solve the problem, we need to find the values of angles A, B, and C given the angles ACE and CAF. Let's break it down step by step.
Step 1: Identify Given Angles
We are given:
- Angle ACE = 43°
- Angle CAF = 62°
Step 2: Find Angle AEC
In triangle ACE, the sum of the angles is 180°. Therefore, we can write the equation:
Angle ACE+Angle CAF+Angle AEC=180°
Substituting the known values:
43°+62°+Angle AEC=180°
Calculating:
Angle AEC=180°−43°−62°
Angle AEC=180°−105°
Angle AEC=75°
Step 3: Find Angle ABD
In cyclic quadrilateral ABDE, we know that the sum of opposite angles is 180°. Thus:
Angle ABD+Angle AEC=180°
Substituting the value of Angle AEC:
Angle ABD+75°=180°
Calculating:
Angle ABD=180°−75°
Angle ABD=105°
So, we have:
A=105°
Step 4: Find Angle B in Triangle ABF
In triangle ABF, the sum of the angles is also 180°. Therefore:
Angle ABF+Angle BAF+Angle AFB=180°
Letting:
- Angle ABF = A (which we found to be 105°)
- Angle BAF = 62° (given)
- Angle AFB = B (unknown)
We can write:
105°+62°+B=180°
Calculating:
B=180°−105°−62°
B=180°−167°
B=13°
So, we have:
B=13°
Step 5: Find Angle C in Triangle ADF
In triangle ADF, the sum of the angles is again 180°. Thus:
Angle ADF+Angle DEF+Angle EFD=180°
Letting:
- Angle ADF = C (unknown)
- Angle DEF = 180° - 75° = 105° (since it is a linear pair with Angle AEC)
- Angle EFD = B = 13° (found earlier)
We can write:
C+105°+13°=180°
Calculating:
C+118°=180°
C=180°−118°
C=62°
So, we have:
C=62°
Final Values
- A = 105°
- B = 13°
- C = 62°
We are given:
- Angle ACE = 43°
- Angle CAF = 62°
In triangle ACE, the sum of the angles is 180°. Therefore, we can write the equation:
Angle ACE+Angle CAF+Angle AEC=180°
43°+62°+Angle AEC=180°
Angle AEC=180°−43°−62°
Angle AEC=180°−105°
Angle AEC=75°
In cyclic quadrilateral ABDE, we know that the sum of opposite angles is 180°. Thus:
Angle ABD+Angle AEC=180°
Angle ABD+75°=180°
Angle ABD=180°−75°
Angle ABD=105°
A=105°
In triangle ABF, the sum of the angles is also 180°. Therefore:
Angle ABF+Angle BAF+Angle AFB=180°
- Angle ABF = A (which we found to be 105°)
- Angle BAF = 62° (given)
- Angle AFB = B (unknown)
105°+62°+B=180°
B=180°−105°−62°
B=180°−167°
B=13°
B=13°
In triangle ADF, the sum of the angles is again 180°. Thus:
Angle ADF+Angle DEF+Angle EFD=180°
- Angle ADF = C (unknown)
- Angle DEF = 180° - 75° = 105° (since it is a linear pair with Angle AEC)
- Angle EFD = B = 13° (found earlier)
C+105°+13°=180°
C+118°=180°
C=180°−118°
C=62°
C=62°
- A = 105°
- B = 13°
- C = 62°
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the given figure, find ∠ABC.

View SolutionIn the given figure, find ∠AOB.

View SolutionIn the adjoining figure ∠QPO=24∘ and ∠SPR=20∘ , find the value of ∠QOR.

View SolutionIn the given figure if find, ∠AOC=45∘, find ∠BOD
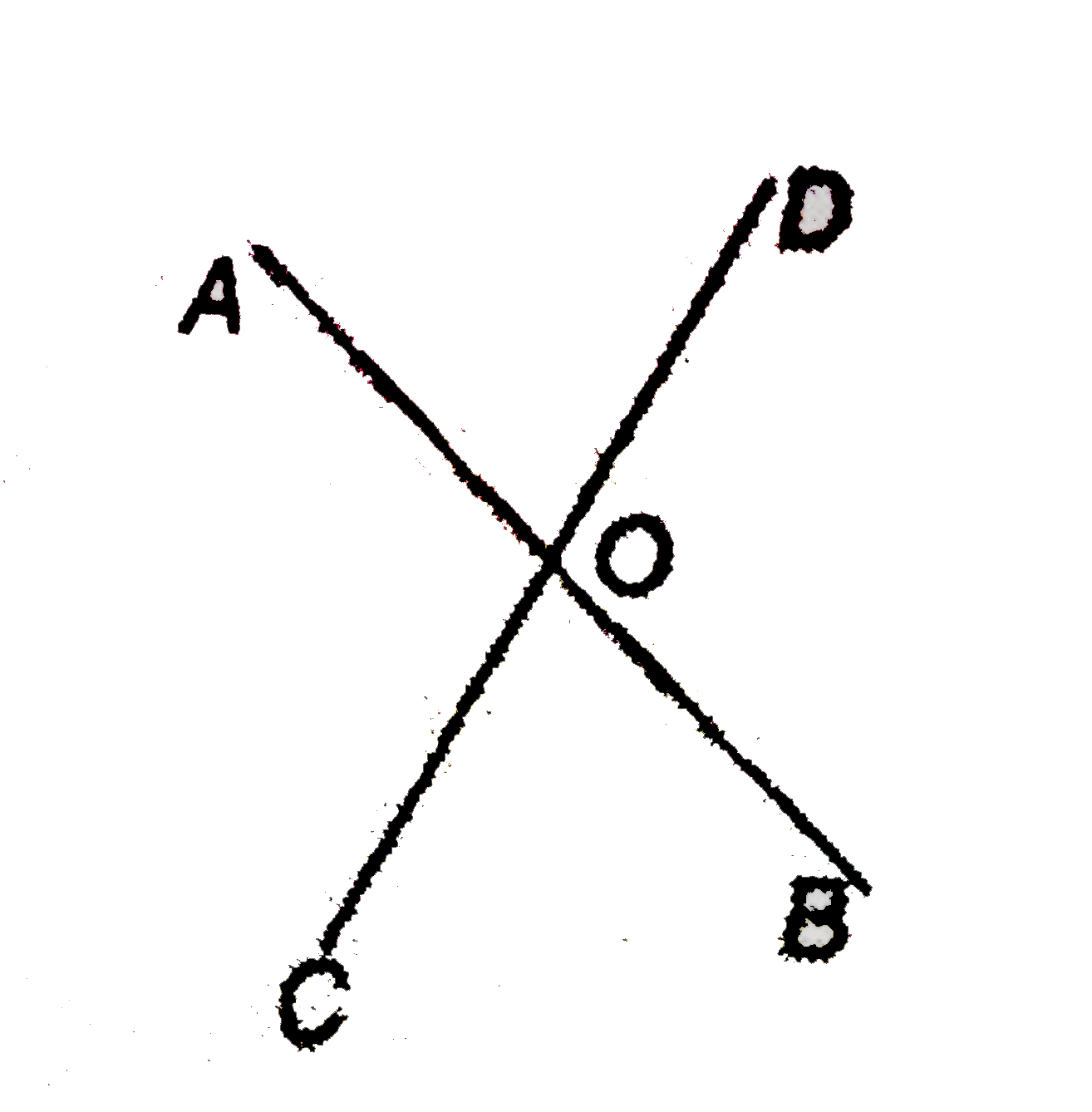
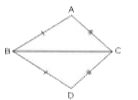
View SolutionIn the given figure, AB = DB and AC = DC. If ∠ABD=58∘,∠DBC=(2x−4)∘,∠ACB=y+15∘and∠DCB=63∘, find the values of x and y.
View SolutionIn the adjoining figure, ∠ABC=95∘ and ∠DAC=35∘, then find the value of ∠ACD.

View SolutionIn the given figure, find ∠D and ∠B.

View SolutionIn the given figure ∠B=90∘and∠ADB=x∘, Find :
(i) sin∠CAB
(ii)cos2C∘+sin2C∘
(iii) tanx∘−cosx∘+3sinx∘

View SolutionIn the given below AB is parallel to CD and CA = CE .
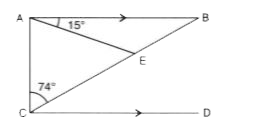
If angle ACE = 74∘and∠EAB=15∘ find the angles AEB and BCD.
View SolutionIn the following figure , AB = AC , EC = ED ∠ABF=45∘and∠ABC=70∘
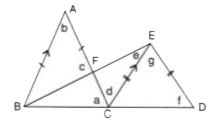
Find the angles represented by letters a,b,c,d,e,f and g.
View Solution
